📃Micro Lie Theory 리뷰

A micro Lie theory for state estimation in robotics

• Paper Link

1. 🎯 이 논문은 로봇 공학 분야의 상태 추정에서 Lie 군 이론을 로봇 공학자들이 더 쉽게 이해하고 활용할 수 있도록 ’마이크로 Lie 이론’으로 단순화하여 제시합니다.
2. 🛠️ 저자들은 Lie 이론의 필수적인 부분만을 선별하고, Exp, Log, ⊕, 와 같은 연산자를 도입하여 Lie 대수 대신 벡터 공간을 활용함으로써 불확실성 관리 및 야코비 행렬 계산을 단순화합니다.
3. 🤖 이 연구는 로봇 위치 추정 및 매핑(SLAM)과 같은 응용 분야에서 Kalman 필터와 그래프 기반 최적화 알고리즘을 통해 제안된 이론의 실용성과 우아함을 시연하며, 관련 C++ 라이브러리(manif)도 제공합니다.

---

1 Brief Review

이 논문은 19세기 수학자 Sophus Lie가 연속 변환 group 이론의 기초를 마련한 이래 다양한 과학 기술 분야로 영향을 확장해 온 수학적 추상체인 Lie group에 대해 다룬다. 특히 로봇 공학 분야에서는 최근 estimation, 그 중에서도 navigation을 위한 motion estimation 분야에서 그 사용이 두드러지고 있다. 하지만 대다수의 로봇 공학자에게 Lie group은 여전히 고도로 추상적인 개념으로 이해하고 사용하기 어렵다.

이 논문은 로봇 공학의 estimation에서 Lie theory의 모든 역량을 활용할 필요는 없다는 점에 착안하여, 이론의 핵심 원리만을 선별하여 명확하고 유용한 아이디어를 전달하고자 한다. 이러한 간소화된 micro Lie theory는 SLAM, 시각 odometry 등 현대 로봇 공학의 estimation algorithm에서 매우 유용함이 입증되었다. 이 micro Lie theory와 함께, 로봇 공학에서 가장 많이 사용되는 주요 Lie group에 대한 공식(대부분의 Jacobian matrix와 이를 쉽게 조작하는 방법 포함)을 참고 자료로 제공한다. 또한, 여기에 설명된 모든 기능을 구현하는 새로운 C++ template-only library인 manif도 소개한다.

I. 서론

최근 로봇 커뮤니티에서는 정밀도, 일관성 및 해법의 안정성에 대한 요구가 증가함에 따라 estimation 문제를 적절하게 공식화하려는 노력이 활발하다. 이는 상태 및 측정값, 이들을 연결하는 함수, 그리고 불확실성을 적절하게 모델링하는 것이 중요하기 때문이다. 이러한 노력은 상태 표현이 진화하는 Lie group의 부드러운 topologic surface인 manifold를 포함하는 설계로 이어졌다. Lie theory(LT)를 활용하여 불확실성, 미분 및 적분을 정밀하고 쉽게 다룰 수 있는 엄격한 계산 체계를 구축할 수 있다. 일반적으로 이러한 작업은 SO(3) 및 SE(3)와 같은 잘 알려진 manifold에 중점을 둔다.

Lie group을 처음 접할 때, 위상학적, 대수적, 기하학적 관점에서 접근하는 것이 중요하다. 위상학적 관점은 manifold의 형태를 다루며 tangent space 및 exponential map과의 관계에 대한 직관을 제공한다. 대수적 관점은 group operation과 구체적인 구현을 포함하여 대수적 속성을 활용하여 폐쇄형 공식을 개발하거나 단순화한다. 로봇 공학에 특히 유용한 기하학적 관점은 group element를 로봇의 위치, 속도, 방향 등과 연결한다.

Lie theory는 결코 간단하지 않다. 이 논문은 기존의 “기본”, “매우 기본”, “순진한” Lie theory 관련 서적들보다 더욱 간소화된 micro Lie theory를 제공한다. 이는 Lie theory에서 로봇 공학의 불확실성 관리에 필요한 작은 부분 집합만을 선별하고, didactic하게 많은 중복을 통해 설명함으로써 Lie theory 진입 장벽을 낮추려는 목적을 가진다. 특히, 대부분의 최적 estimator에 필수적이지만 구현에 어려움을 겪는 Jacobian 계산에 중점을 둔다. 이 논문은 새로운 open-source C++ header-only library인 manif(https://github.com/artivis/manif)와 함께 제공된다. manif는 널리 사용되는 SO(2), SO(3), SE(2), SE(3) group을 구현하며 analytic Jacobian 생성을 지원한다.

II. A MICRO LIE THEORY

A. Lie Group

Lie group은 group과 smooth manifold의 개념을 통합한 것으로, group axiom을 만족하는 smooth manifold이다. smooth manifold는 국소적으로 linear space와 유사한 topological space로, 곡면이지만 가장자리나 뾰족한 부분이 없는 부드러운 (hyper)-surface로 시각화될 수 있다. manifold의 부드러움은 각 지점에 고유한 tangent space가 존재함을 의미한다. group axiom은 다음과 같다:

• Closure under ◦: X \circ Y \in G (1)
• Identity E: E \circ X = X \circ E = X (2)
• Inverse X^{-1}: X^{-1} \circ X = X \circ X^{-1} = E (3)
• Associativity: (X \circ Y) \circ Z = X \circ (Y \circ Z) (4)
• Lie group에서는 모든 tangent space가 동일한 구조를 가지며, group structure는 manifold 요소들의 합성 결과가 manifold 내에 유지되고, 각 요소가 manifold 내에 inverse를 가지도록 한다. identity에서의 tangent space를 Lie algebra라고 한다.

B. Group Action

Lie group은 다른 set의 요소들을 변환하는 기능을 제공하며, 이는 로봇 공학에서 rotation, translation, scaling 등에 광범위하게 사용된다. Lie group M과 set V가 주어졌을 때, X \in M의 v \in V에 대한 action은 X \cdot v로 표기하며 다음 axiom을 만족해야 한다: - Identity: E \cdot v = v (6) - Compatibility: (X \circ Y) \cdot v = X \cdot (Y \cdot v) (7) 일반적인 예로는 rotation matrices SO(n), unit quaternions group, rigid motion group SE(n) 등이 있다.

C. Tangent Space와 Lie Algebra

Lie group의 manifold M 위를 움직이는 점 X(t)의 속도 \dot{X} = \partial X / \partial t는 X에서의 tangent space T_X M에 속한다. manifold의 부드러움은 각 지점에 고유한 tangent space가 존재함을 의미한다.

1. Lie algebra \mathfrak{m}: identity E에서의 tangent space T_E M를 Lie algebra \mathfrak{m}이라 한다: \mathfrak{m} \triangleq T_E M (8). 모든 Lie group에는 관련된 Lie algebra가 있다. Lie algebra \mathfrak{m}은 vector space이다. 그 요소들은 M의 자유도 m에 해당하는 m차원 vector로 식별될 수 있다. exponential map \text{exp}: \mathfrak{m} \to M은 Lie algebra의 요소를 group의 요소로 정확히 변환한다. log map은 역 연산이다. multiplicative group의 경우, Lie algebra의 요소들은 v^\wedge = X^{-1} \dot{X} = -\dot{X}^{-1} X (9)와 같은 형태로 얻을 수 있다.
2. Cartesian vector space \mathbb{R}^m: Lie algebra 요소 \tau^\wedge는 skew-symmetric matrices, imaginary numbers, pure quaternions와 같은 비자명한 구조를 가지지만, 이는 m개의 generator E_i의 linear combination으로 표현될 수 있다. Hat 및 Vee(\vee)라는 두 개의 상호 역 linear map 또는 isomorphism을 통해 \mathfrak{m}에서 \mathbb{R}^m으로, 그 반대로 변환할 수 있다: Hat: \mathbb{R}^m \to \mathfrak{m}; \tau \mapsto \tau^\wedge = \sum_{i=1}^m \tau_i E_i (10) Vee: \mathfrak{m} \to \mathbb{R}^m; \tau^\wedge \mapsto (\tau^\wedge)^\vee = \tau = \sum_{i=1}^m \tau_i e_i (11) 따라서 \mathfrak{m}은 \mathbb{R}^m과 isomorphic하다 (\mathfrak{m} \cong \mathbb{R}^m). 이 논문에서는 \mathfrak{m}보다 \mathbb{R}^m을 선호하며, 모든 연산자 (adjoint, Jacobian, perturbation, covariance matrix)는 \mathbb{R}^m에 대해 정의된다.

D. Exponential Map

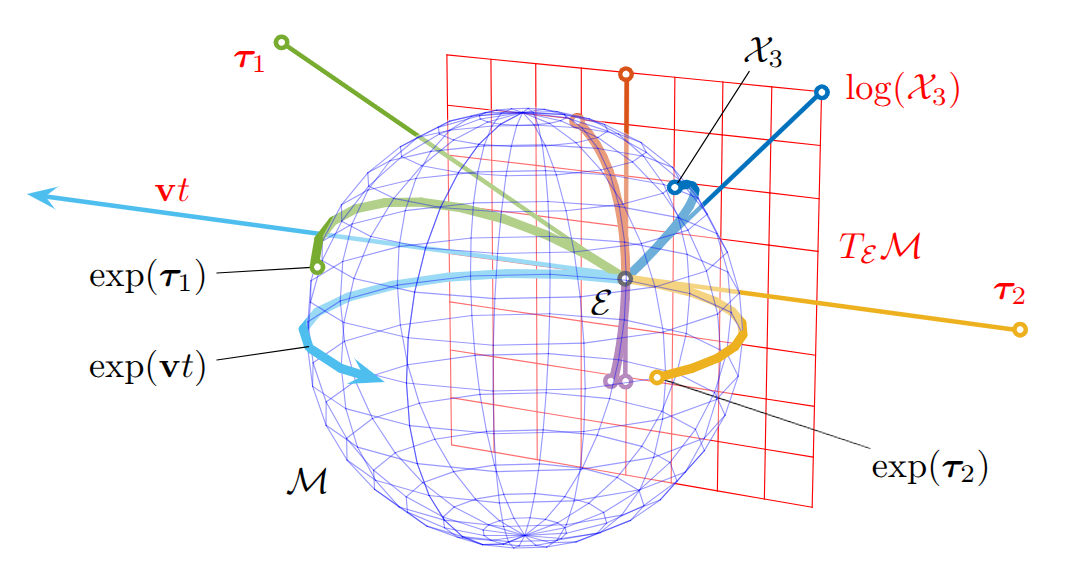
exponential map \text{exp}(\cdot)은 Lie algebra의 요소를 group으로 정확히 변환하는 retraction 연산이다. 직관적으로 exp()는 tangent element를 geodesic을 따라 manifold 주위로 감싼다. 역 map은 log()이다. \dot{X} = X v^\wedge (12) 이 ODE의 해는 X(t) = X(0) \text{exp}(v^\wedge t) (13)이다.

exponential map과 그 역 logarithmic map은 다음과 같이 쓸 수 있다: \text{exp}: \mathfrak{m} \to M; \tau^\wedge \mapsto X = \text{exp}(\tau^\wedge) (14) \text{log}: M \to \mathfrak{m}; X \mapsto \tau^\wedge = \text{log}(X) (15)

폐쇄형 exponential map은 absolutely convergent Taylor series를 사용하여 얻을 수 있다. Capitalized Exp와 Log maps: Exp와 Log map은 vector element \tau \in \mathbb{R}^m를 M의 요소 X에 직접 매핑하는 편리한 단축키이다. X = \text{Exp}(\tau) \triangleq \text{exp}(\tau^\wedge) (23) \tau = \text{Log}(X) \triangleq (\text{log}(X))^\vee (24)

E. Plus 및 Minus 연산자

Plus(\oplus) 및 Minus(\boxminus) 연산자는 curved manifold의 요소들 사이에 증분을 도입하고 이를 flat tangent vector space에서 표현할 수 있도록 한다. 이들은 Exp/Log 연산과 composition을 결합한다. composition의 비가환성 때문에, 피연산자의 순서에 따라 right- 및 left- 버전으로 정의된다.

• right-⊕: Y = X \oplus X_\tau \triangleq X \circ \text{Exp}(X_\tau) \in M (25)
• right-boxminus: X_\tau = Y \boxminus X \triangleq \text{Log}(X^{-1} \circ Y) \in T_X M (26)
• left-⊕: $Y = E_\tau \oplus X \triangleq \text{Exp}(E_\tau) \circ X \in M (27)
• left-boxminus: E_\tau = Y \boxminus X \triangleq \text{Log}(Y \circ X^{-1}) \in T_E M (28)

이 논문에서는 기본적으로 perturbation을 국소적으로 표현하기 위해 right 형태의 ⊕ 및 \boxminus를 사용한다.

F. Adjoint 및 Adjoint Matrix

Eτ ⊕ X = X ⊕ Xτ를 통해 국소(local) tangent element와 전역(global) tangent element 사이의 관계를 파악할 수 있다. - Adjoint: M의 X에 대한 Adjoint는 \text{Ad}_X: \mathfrak{m} \to \mathfrak{m}; \tau^\wedge \mapsto \text{Ad}_X (\tau^\wedge) \triangleq X \tau^\wedge X^{-1} (29)로 정의되어 E_\tau^\wedge = \text{Ad}_X (X_\tau^\wedge)를 만족한다. - Adjoint matrix: \text{Ad}_X는 linear이므로, Cartesian tangent vector E_\tau \cong E_\tau^\wedge와 X_\tau \cong X_\tau^\wedge를 매핑하는 동등한 matrix operator \text{Ad}_X를 찾을 수 있다: \text{Ad}_X: \mathbb{R}^m \to \mathbb{R}^m; X_\tau \mapsto E_\tau = \text{Ad}_X X_\tau (30) 이는 (\text{Ad}_X \tau = (X \tau^\wedge X^{-1})^\vee) (31)를 개발하여 계산할 수 있다. Adjoint matrix는 X에서의 tangent space의 vector를 origin에서의 tangent space의 vector로 linear하게 변환하는 데 자주 사용된다.

G. Lie Group에서의 미분

Lie group에서의 미분은 주로 vector tangent space를 매핑하는 Jacobian matrix 형태로 정의된다. 이는 불확실성과 증분을 적절하고 쉽게 정의할 수 있기 때문이다. 이러한 Jacobian을 사용하면 Lie group의 불확실성 관리 공식이 vector space의 공식과 크게 유사해진다.

1. Vector space에서의 Jacobian: 함수 f: \mathbb{R}^m \to \mathbb{R}^n에 대해 Jacobian matrix는 모든 편미분을 쌓은 n \times m matrix이다: J = \frac{\partial f(x)}{\partial x} \triangleq \begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_m} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \cdots & \frac{\partial f_n}{\partial x_m} \end{pmatrix} \in \mathbb{R}^{n \times m} (35) Jacobian은 J = \frac{\partial f(x)}{\partial x} = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \in \mathbb{R}^{n \times m} (38)과 같이 정의할 수 있다.
2. Lie group에서의 Right Jacobian: manifold에서 작동하는 함수 f: M \to N의 Jacobian을 정의하기 위해 ⊕ 및 \boxminus 연산자를 사용할 수 있다: ^X D_X f(X) \triangleq \lim_{\tau \to 0} \frac{f(X \oplus \tau) \boxminus f(X)}{\tau} \in \mathbb{R}^{n \times m} (41a) 이를 right Jacobian이라 부른다. 이는 X와 f(X)에서의 국소 tangent space의 vector로 표현된 무한소 변화량의 미분이다.
3. Lie group에서의 Left Jacobian: left plus 및 minus operator에서 미분을 정의할 수도 있다: ^E D_X f(X) \triangleq \lim_{\tau \to 0} \frac{f(\tau \oplus X) \boxminus f(X)}{\tau} \in \mathbb{R}^{n \times m} (44) 이를 left Jacobian이라 부른다. 이는 global tangent space(Lie algebra)를 매핑하는 matrix이다. left Jacobian과 right Jacobian은 adjoint에 의해 관련된다: ^E D_X f(X) \text{Ad}_X = \text{Ad}_{f(X)} ^X D_X f(X) (46)

H. Manifold에서의 불확실성, Covariance Propagation

점 \bar{X} \in M 주변의 국소 perturbation \tau는 tangent vector space T_{\bar{X}} M에서 right-⊕ 및 \boxminus를 사용하여 정의된다: X = \bar{X} \oplus \tau, \tau = X \boxminus \bar{X} \in T_{\bar{X}} M (51) Covariance matrix는 이 tangent space에서 expectation operator E[·]를 통해 적절하게 정의될 수 있다: \Sigma_X \triangleq E[\tau \tau^>] = E[(X \boxminus \bar{X})(X \boxminus \bar{X})^>] \in \mathbb{R}^{m \times m} (52) 이를 통해 manifold에 Gaussian variable X \sim N(\bar{X}, \Sigma_X)를 정의할 수 있다. global 및 local perturbation은 adjoint (30)에 의해 관련되므로, covariance는 다음과 같이 변환될 수 있다: ^E \Sigma_X = \text{Ad}_X {}^X \Sigma_X \text{Ad}_X^> (54) 함수 f: M \to N; X \mapsto Y = f(X)를 통한 covariance propagation은 Jacobian matrix (41a)를 사용한 linearization (43)을 통해 익숙한 공식을 제공한다: \Sigma_Y \approx {}^X D_X f \Sigma_X {}^X D_X f^> \in \mathbb{R}^{n \times n} (55)

I. Manifold에서의 이산 적분

exponential map X(t) = X_0 \circ \text{Exp}(vt)는 manifold 위에서 일정 속도 v \in T_{X_0} M의 연속 시간 적분을 수행한다. 비일정 속도 v(t)는 일반적으로 piecewise constant bit v_k \in T_{X_{k-1}} M와 짧은 지속 시간 \delta t_k로 분할하여 이산 적분으로 구성된다: X_k = X_{k-1} \oplus \tau_k = X_{k-1} \circ \text{Exp}(\tau_k) = X_{k-1} \circ \text{Exp}(v_k \delta t_k) (56)

III. MANIFOLD에서의 미분 규칙

일반적인 manifold에 대해, inversion, composition, exponentiation 및 action에 대한 기본 Jacobian의 폐쇄형을 결정할 수 있다. 또한, 이들 중 일부는 adjoint \text{Ad}_X와 관련될 수 있으며, 이는 미분 과정의 핵심 block이 된다. 다른 Log, ⊕, \boxminus에 대한 형태는 이들로부터 쉽게 파생될 수 있다.

A. Chain Rule

Y = f(X)이고 Z = g(Y)일 때, Z = g(f(X))이다. chain rule은 다음과 같다: D_X Z = D_Y Z D_X Y 또는 J_X^Z = J_Y^Z J_X^Y (58)

B. 기본 Jacobian Block

1. Inverse: J_X^{X^{-1}} = - \text{Ad}_X (62)
2. Composition: J_X^{X \circ Y} = \text{Ad}_{Y^{-1}} (65), J_Y^{X \circ Y} = I (66)
3. Jacobians of M: Exp map의 right Jacobian은 J_r(\tau) \triangleq {}^\tau D_\tau \text{Exp}(\tau) \in \mathbb{R}^{m \times m} (67)로 정의된다. left Jacobian은 J_l(\tau) \triangleq {}^E D_\tau \text{Exp}(\tau) \in \mathbb{R}^{m \times m} (71)로 정의된다. right Jacobian과 left Jacobian은 adjoint에 의해 관련된다: \text{Ad}_{\text{Exp}(\tau)} = J_l(\tau) J_r^{-1}(\tau) (75)
4. Group action: X \in M 및 v \in V에 대한 Jacobian은 J_X^{X \cdot v} = {}^X D_X X \cdot v (77) 및 J_v^{X \cdot v} = {}^v D_v X \cdot v (78)로 정의된다.

C. 유도된 Jacobian Block

1. Log map: J_X^{\text{Log}(X)} = J_r^{-1}(\tau) (79)
2. Plus 및 Minus: J_X^{X \oplus \tau} = \text{Ad}_{\text{Exp}(\tau)^{-1}} (80) J_\tau^{X \oplus \tau} = J_r(\tau) (81) J_X^{Y \boxminus X} = -J_l^{-1}(\tau) (82) J_Y^{Y \boxminus X} = J_r^{-1}(\tau) (83)

IV. Composite Manifold

Composite manifold M = \langle M_1, \cdots, M_M \rangle는 M개의 상호작용하지 않는 manifold의 연결이다. 이는 각 block에 대해 identity, inverse, composition을 별도로 정의함으로써 이루어진다. Exp와 Log map 또한 각 block에 대해 독립적으로 정의된다: \text{Exp}\langle\tau\rangle \triangleq \begin{pmatrix} \text{Exp}(\tau_1) \\ \vdots \\ \text{Exp}(\tau_M) \end{pmatrix}, \text{Log}\langle X \rangle \triangleq \begin{pmatrix} \text{Log}(X_1) \\ \vdots \\ \text{Log}(X_M) \end{pmatrix} (85) 이는 composite의 right-plus 및 minus 연산자를 생성한다: X \boxplus \tau \triangleq X \diamond \text{Exp}\langle\tau\rangle (86) Y \boxminus X \triangleq \text{Log}\langle X^{-1} \diamond Y \rangle (87) 이를 통해 새로운 미분을 정의할 수 있다: \frac{D f(X)}{D X} \triangleq \lim_{\tau \to 0} \frac{f(X \boxplus \tau) \boxminus f(X)}{\tau} (88) composite manifold에서 작동하는 함수 f: M \to N의 Jacobian은 block-wise로 결정될 수 있다.

V. LANDMARK-BASED LOCALIZATION 및 MAPPING

이론의 적용 예시로 로봇 localization 및 mapping을 제공한다. 로봇 자세는 SE(2)(App. C)에, beacon 위치는 R2(App. E)에 존재한다. control signal u는 longitudinal velocity v와 angular velocity ω를 포함하는 se(2)의 twist이다. landmark 측정값은 range 및 bearing type이지만 단순화를 위해 Cartesian form으로 표현된다. A. Manifold에서의 Error-State Kalman Filter를 이용한 Localization beacon의 위치가 알려져 있다고 가정하고, 추정할 자세는 \hat{X} \in \text{SE(2)}로 정의한다. 추정 오차 \delta x와 그 covariance P는 tangent space에서 (51), (52)를 사용하여 표현된다. \delta x \triangleq X \boxminus \hat{X} \in \mathbb{R}^3 (97) P \triangleq E[(X \boxminus \hat{X})(X \boxminus \hat{X})^>] \in \mathbb{R}^{3 \times 3} (98) 로봇의 움직임마다 ESKF prediction을 적용한다: \hat{X}_j = \hat{X}_i \oplus u_j (99) P_j = F P_i F^> + G W_j G^> (100) beacon 측정값 y_k마다 ESKF correction을 적용한다: State update: \hat{X} \leftarrow \hat{X} \oplus \delta x (101) Covariance update: P \leftarrow P - K Z K^> (102) 정규 EKF와의 유일한 차이점은 (99)와 (101)에서 정규 +가 ⊕로 대체된다는 점이다. Jacobian은 모두 Lie theory를 사용하여 계산된다.

B. Graph-based Optimization을 이용한 Smoothing 및 Mapping

SAM(smoothing and mapping) 문제는 beacon의 위치와 로봇의 궤적을 추정하는 것으로, graph-based iterative least-squares optimizer를 사용한다. 문제 상태는 composite X = \langle X_1, X_2, X_3, b_4, b_5, b_6 \rangle로 표현된다. 각 prior 또는 측정은 그래프에 factor를 기여한다. 최적화 단계 \delta x^*는 \delta x^* = \arg \min_{\delta x} \sum_{p \in \mathcal{P}} r_p(X \boxplus \delta x)^> r_p(X \boxplus \delta x) (106)를 최소화하여 얻어진다. 각 residual은 Jacobian을 사용하여 선형화된다. 이 문제는 least-squares를 사용하여 \delta x^* = -(J^> J)^{-1} J^> r (109)로 해결되며, 이 optimal step \delta x^*는 상태를 업데이트하는 데 사용된다: X \leftarrow X \boxplus \delta x^* (110). 이 과정은 수렴할 때까지 반복된다. composite notation의 사용은 Jacobian의 block-wise 정의와 업데이트를 가능하게 한다.

C. Self-calibration을 포함한 Smoothing 및 Mapping

움직임 센서가 알 수 없는 calibration bias c = (c_v, c_\omega)^>에 영향을 받는다고 가정하면, control은 이제 \tilde{u} = (v \delta t + c_v, 0, \omega \delta t + c_\omega)^> + w가 된다. 상태 composite는 알 수 없는 c로 확장된다. 최적 솔루션은 센서 bias의 최적 추정치를 포함한다.

D. 3D 구현

위의 모든 예시는 3D로 쉽게 확장될 수 있다. 모든 변수를 올바른 space(X \in \text{SE(3)}, u \in \mathbb{R}^6 \cong \text{se(3)}, 그리고 \{b_k, y\} \in \mathbb{R}^3)에 정의하는 것으로 충분하다. Jacobian과 covariance matrix도 적절한 크기로 조정된다. Lie theory가 제공하는 추상화 수준 덕분에 2D와 3D에 대해 알고리즘의 모든 수학적 내용은 정확히 동일하다는 점이 중요하다.

VI. 결론

이 논문은 상태 추정에 능숙한 독자층, 특히 로봇 공학 응용 분야에 유용한 형태로 Lie theory의 필수적인 부분을 제시한다. 첫째, 가능한 한 추상적인 수학적 개념을 피하는 자료 선별을 통해 Lie theory의 도구를 이해하고 사용하기 쉽게 만들었다. 둘째, 상당한 중복을 포함한 didactical approach를 선택했다. 본문은 Lie theory의 추상적인 점들을 다루며, 구체적인 Lie group에 추상적인 개념을 적용하는 예시와 상세한 설명을 포함하는 그림들이 함께 제공된다. 셋째, capitalized Exp() 및 Log() map과 plus, minus operator(⊕, \boxminus, \boxplus, \boxminus)와 같은 편리한 연산자 사용을 권장했다. 이를 통해 tangent space의 Cartesian representation에서 작업할 수 있으며, 표준 vector space의 공식과 크게 유사한 미분 및 covariance 처리 공식을 생성한다. 넷째, Jacobian의 정의, 기하학적 해석 및 계산에 특별히 강조했다. 이를 위해 Jacobian matrix와 covariance에 대한 표기법을 도입하여 시각적으로 강력한 조작을 가능하게 했다. 특히 chain rule은 이 표기법으로 명확하게 보인다. 다섯째, 부록에서 로봇 공학에서 가장 일반적으로 사용되는 group에 대한 광범위한 공식 모음을 제시한다. 여섯째, Lie theory가 로봇 공학 문제를 우아하고 정밀하게 해결하는 능력을 보여주는 몇 가지 응용 예시를 제시했다. 마지막으로, 이 논문은 여기에 설명된 도구를 구현하는 새로운 C++ 라이브러리 manif를 함께 제공한다. 이 논문은 새로운 이론적 내용을 도입하지는 않지만, Lie theory가 제시된 방식이 많은 연구자가 향후 개발을 위해 이 분야에 진입하는 데 도움이 될 것이라고 믿는다.

---

2 Detail Review

로봇 상태 추정과 Lie 이론: 이론과 응용의 직관적 해설

로봇 공학의 상태 추정 문제에서는 Lie 군을 통한 표현이 갈수록 중요해지고 있습니다. 그러나 많은 로봇공학자들에게 Lie 이론은 여전히 추상적으로 느껴지곤 합니다. 이 글에서는 Joan Solà 등이 발표한 “A micro Lie theory for state estimation in robotics” 논문의 내용을 기반으로, Lie 군과 Lie 대수의 핵심 개념을 복습하고 이를 로봇 상태 추정에 적용하는 방법을 설명하겠습니다. 특히 retraction (\oplus 연산), perturbation (오차 표현), Jacobian 계산을 중심으로, 기존의 유클리드 공간 기반 필터와 무엇이 다른지, 또 어떤 이점이 있는지 수식과 함께 상세히 해설합니다.

2.1 Lie 군과 Lie 대수 기본 개념 복습

Lie 군(Lie group)은 매끄러운(manifold) 곡면 위에 그룹 구조를 결합한 수학 객체입니다. 구체적으로, Lie 군 G는 미분 가능한 매니폴드(국소적으로 평탄한 공간)로서 그 원소들이 그룹의 네 가지 공리(폐쇄성, 항등원, 역원, 결합법칙)를 만족합니다. 다시 말해, Lie 군은 국소적으로는 선형 공간처럼 미분 연산이 가능하면서도 전역적으로는 비선형 결합(composition)이 허용되는 구조를 갖습니다. 대표적인 예로 3차원 회전의 공간 SO(3)나 로봇 자세(pose)를 나타내는 SE(3) 등이 있습니다.

매니폴드란 국소적으로 유클리드 공간과 유사하지만 전역적으로는 곡률 등의 제약이 있는 공간입니다. 예를 들어, 단위 노름을 갖는 4차원 벡터들의 집합(유니터니언)은 4차원 구면 S^3을 이루며, 이는 단위 쿼터니언의 공간이 됩니다. 이처럼 로봇 상태가 충족해야 할 제약(예: 쿼터니언의 단위 노름)은 매니폴드를 정의하며, 우리의 상태 벡터는 이 매끄러운 곡면 위를 움직인다고 볼 수 있습니다. 중요한 점은, 매니폴드 위의 모든 점마다 고유한 접공간(tangent space)이 존재하고, 이 접공간은 그 점을 스쳐 지나가는 평면으로 이해할 수 있습니다. 접공간은 선형 벡터 공간이므로 우리가 그 위에서는 미분이나 선형대수 계산을 자유롭게 할 수 있습니다.

한편, Lie 군에는 한 특별한 원소(항등원 E)와 그에 대응하는 접공간이 존재합니다. 이를 Lie 대수(Lie algebra)라고 부르며, 기호로 \mathfrak{g}=T_E G로 나타냅니다. Lie 대수는 차원이 Lie 군의 자유도와 같고, 항등원에서의 접공간이기 때문에 벡터 공간의 구조를 가집니다. 특히 Lie 대수의 원소들은 종종 \mathbb{R}^n의 벡터로 간주할 수 있는데, 이는 \mathfrak{g} \simeq \mathbb{R}^n (벡터 공간으로 동형)이라는 의미입니다. 예를 들어 회전군 SO(3)의 Lie 대수인 so(3)은 3\times3 반대칭 행렬들의 공간이지만, 이를 축각(axis-angle) 3-벡터로 대응시킬 수 있어서 \mathbb{R}^3와 동형입니다. 이러한 벡터와 행렬 간 변환을 편리하게 하기 위해 해트 연산(^\wedge)과 브이 연산(^\vee)이 사용됩니다. 3-벡터 \omega = [\omega_x,\omega_y,\omega_z]^\top에 대해 해트 연산은 so(3)의 원소인 [\omega]_\times (skew-symmetric matrix)을 만들고, 브이 연산은 그 반대로 행렬을 벡터로 돌려놓습니다. 이를 통해 Lie 대수 원소와 유클리드 벡터를 자유롭게 넘나들며 계산할 수 있습니다.

이제 지수 맵(Exponential)과 로그 맵(Logarithm)을 소개합니다. 지수 맵 \text{Exp}: \mathfrak{g} \to G는 Lie 대수의 원소(접공간의 벡터)를 Lie 군의 원소로 변환하는 함수이고, 로그 맵 \text{Log}: G \to \mathfrak{g}는 그 역변환입니다. 이는 일반적인 행렬 지수함수(\text{Exp})로 정의되며, 작은 변화량을 곡면 위의 유한한 움직임으로 바꿔주는 역할을 합니다. 예를 들어 so(3)에서 \text{Exp}([\omega]_\times)는 \omega만큼 회전하는 회전행렬 R을 생성하며, 이는 로드리게스 공식으로 주어집니다. 로드리게스 공식에 따르면 |\omega|를 회전 크기로 할 때:

\text{Exp}_{SO(3)}(\omega^\wedge) = I + \frac{\sin\|\omega\|}{\|\omega\|}[\omega]_\times + \frac{1-\cos\|\omega\|}{\|\omega\|^2}[\omega]_\times^2,

이는 \omega가 충분히 작을 때 \text{Exp}(\omega^\wedge) \approx I + [\omega]_\times로 근사되며 익숙한 소(小)각도 근사와 일치합니다. 마찬가지로 \text{Log}(R)는 주어진 군 원소를 다시 Lie 대수의 벡터(회전벡터)로 돌려놓습니다. 즉, \text{Exp}와 \text{Log} 덕분에 비선형 곡면인 Lie 군과 선형 공간인 Lie 대수를 서로 연결할 수 있으며, Lie 군상의 문제를 Lie 대수상의 문제로 변환해서 풀 수 있게 됩니다. 이러한 변환을 활용하면, 복잡한 제약을 직접 다루는 대신 간단한 선형 공간에서 계산을 수행한 뒤 결과를 다시 매니폴드로 옮기는 방법이 가능해집니다. Solà 등의 논문이 제시하는 “micro Lie theory” 역시 Lie 군의 깊은 이론 중 실용적인 핵심만 뽑아 쓴 것으로, Lie 군과 Lie 대수를 왕복하는 기본 도구들만으로도 로봇 상태 추정에 충분한 정밀도를 얻을 수 있음을 보여줍니다.

2.2 상태 추정에서의 Manifold 상태 표현과 \oplus 연산 (Retraction)

로봇의 상태가 유클리드 공간 \mathbb{R}^n에 국한되지 않고 곡면 위에 놓이는 경우, 이를 다루기 위해 특수한 연산이 필요합니다. 예를 들어 드론의 자세(orientation)를 나타내는 단위 쿼터니언은 4차원 벡터이지만 항상 단위 노름을 가져야 하므로 임의의 4차원 변화량을 더할 수 없습니다. 이 때 사용하는 개념이 바로 Lie 군상의 retraction, 즉 \oplus 연산입니다. 유클리드 공간에서 상태 업데이트를 x_{\text{new}} = x_{\text{old}} + \Delta x로 한다면, Lie 군에서는 이를 대체하는 연산으로 X_{\text{new}} = X_{\text{old}} \oplus \Delta를 정의하는 것입니다. Solà 논문에서는 이를 플러스(\oplus) 연산자로 표기하며, 한 번의 지수 맵(Exp)과 군 합성(\circ)으로 구현됩니다. 구체적으로 오른쪽 플러스 (right-⊕)를 기준으로 하면 다음과 같습니다:

Y = X \oplus \delta := X \circ \text{Exp}(\delta), \qquad \delta = Y \ominus X := \text{Log}(X^{-1}\circ Y).

즉, Lie 군 원소 X에 접공간의 작은 벡터 \delta를 지수맵으로 군 원소화한 \text{Exp}(\delta)를 오른쪽에서 곱해 새로운 원소 Y를 얻는 것이 X\oplus\delta입니다. 반대로 두 원소 Y, X \in G 사이의 “차이”를 나타내는 마이너스(\ominus) 연산 Y \ominus X는 X^{-1}Y라는 군 연산의 결과를 로그맵으로 벡터화한 것입니다. 이러한 \oplus, \ominus 연산자를 도입함으로써, Lie 군상에서 일반 덧셈이 불가능한 경우에도 마치 벡터 더하기/빼기처럼 상태의 합성과 차이를 표현할 수 있습니다. 특히 \oplus 연산은 retraction(리트랙션)으로 볼 수 있는데, 이는 최적화나 필터링 맥락에서 국소 좌표계로 이동했다가 다시 매니폴드로 복원하는 함수를 의미합니다. 여기서는 정확한 지수맵 \text{Exp}를 사용하여 retraction을 구현하므로, 매우 엄밀한 방식으로 상태를 업데이트하게 됩니다.

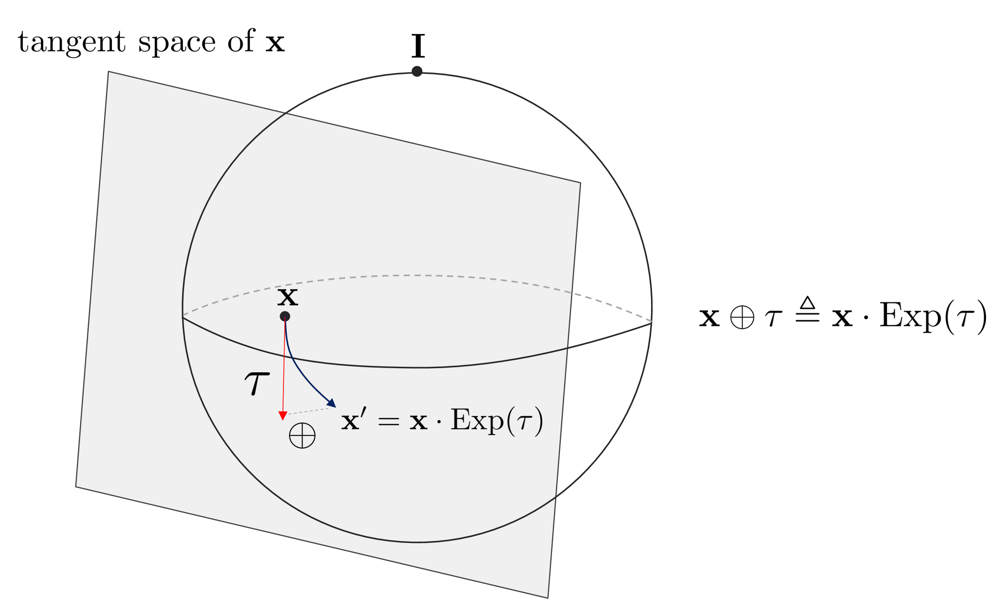
예를 들어, 위 그림은 매니폴드 곡면 (예: 단위 구면) 위의 한 상태 X에 대해 \oplus 연산의 기하학적 의미를 보여줍니다. 점 X가 매니폴드 위에 주어졌을 때, 그 접평면(회색) 위의 한 벡터 \tau (빨간 화살표)를 취해 지수맵을 적용하면 곡면 위의 한 점으로 사상됩니다. X \oplus \tau = X \cdot \text{Exp}(\tau)의 결과로 얻어진 새로운 점 X'이 파란 화살표의 머리로 표시되어 있습니다. 이 과정은 곡면 위의 X에서 시작하여 접공간을 따라 \tau만큼 움직였다가 다시 곡면으로 돌아오는 동작에 해당합니다. 즉, \tau가 작다면 X'는 X에서 조금 이동한 위치가 되며, 항상 곡면 위에 머무르기 때문에 상태 제약이 자동으로 유지됩니다. 그림 상단의 I는 군의 항등원으로, 이때 \tau가 항등원 근처(글로벌 기준)와 X 근처(로컬 기준)에서 동일하게 취급됨을 시사합니다. 이는 Lie 군에서는 모든 접공간이 본질적으로 동일한 구조를 가지기 때문이며, 곧 설명할 좌/우 플러스의 차이와 Adjoint와도 연결되는 개념입니다.

\oplus 연산에는 오른쪽-플러스와 왼쪽-플러스 두 가지 버전이 있습니다. 이는 Lie 군의 비가환성(non-commutativity) 때문에 발생하는 구분으로, 변화량을 왼쪽에서 곱하느냐 오른쪽에서 곱하느냐에 따라 달라집니다. 예를 들어 오른쪽-플러스에서는 X \oplus \delta = X\text{Exp}(\delta)인 반면, 왼쪽-플러스는 X \oplus^L \delta = \text{Exp}(\delta)X와 같이 정의될 수 있습니다. 두 방식 모두 허용되지만, 논문에서는 로컬 좌표계에서의 표현에 맞게 오른쪽-플러스를 기본으로 사용합니다. 쉽게 말해, 현재 추정값 X를 기준 좌표로 삼고 그 접공간에서 오차를 표현하는 방식을 택한 것입니다. 이렇게 하면 X 자체가 변할 때 접공간도 함께 움직이므로 (접평면이 항상 X에 붙어다님), 오차의 해석이 국소적으로 이루어집니다. 다른 문헌에서는 항등원에 대한 전역 좌표로 오차를 표현하기도 하지만, 그 경우에도 두 표현은 Adjoint 변환으로 상호 변환 가능함이 알려져 있습니다. 즉, 전역적인 오차 \delta_E와 국소적인 오차 \delta_X 사이에는 \delta_X = \text{Ad}_X^{-1},\delta_E 관계가 있으며, 공분산 등의 변환에도 활용됩니다. Solà 등의 설명에 따르면 이 논문 및 여러 최신 방법들은 로컬 perturbation X \oplus \delta를 사용하며, 만약 다른 접근법에서 전역 오차(E \oplus \delta 형태)를 사용하더라도 최종 결과에서 차이는 Adjoint로 보정될 수 있습니다.

정리하자면, \oplus 연산은 현재 상태에 작은 Lie 대수 오차를 적용하여 상태를 업데이트하는 연산이며, 이를 통해 필터나 최적화에서 항상 유효한 상태 (Lie 군 원소)를 유지할 수 있습니다. 반대로 \ominus 연산은 두 상태 간의 상대적인 오차를 Lie 대수 벡터로 산출하여 접공간상의 차로 표현해줍니다. 이 두 연산을 도입함으로써 우리는 마치 유클리드 공간에서 하듯 상태를 더하고 빼며 오차를 정의할 수 있게 되었고, 이러한 아이디어는 오차 상태(error-state) 칼만 필터로도 불리는 현대 로봇 상태 추정 필터들의 토대가 되었습니다.

2.3 Lie 이론을 활용한 상태 추정: 오차 표현과 필터 구성

이제 위에서 정의한 \oplus, \ominus 개념을 실제 칼만 필터와 같은 상태 추정 문제에 어떻게 적용하는지 알아보겠습니다. 핵심 아이디어는 참된 상태(true state)와 추정 상태(estimate) 사이의 오차(perturbation)를 Lie 대수의 벡터로 표현하고 추적하는 것입니다. 예를 들어, 추정값을 X (Lie 군의 원소)라 하고 실제 값을 X^*라고 하면, 두 상태 간 오차를 다음과 같이 정의할 수 있습니다:

\tilde{\xi} := X^* \ominus X = \text{Log}(X^{-1} X^*) \in \mathfrak{g},

여기서 \tilde{\xi}는 Lie 대수상의 작은 벡터로서, 추정에서 실제로 가는 “오차 상태”를 나타냅니다. X^* = X \oplus \tilde{\xi}로 풀어쓰면 X^* = X \text{Exp}(\tilde{\xi})가 되며, 실제 상태는 추정 상태에 작은 지수 이동을 가한 것으로 표현됩니다. 이 오차 벡터를 상태로 삼아 칼만 필터를 수행하면, 필터의 추정은 항상 X 주변의 국소 선형 공간에서 이루어집니다. 다시 말해, 필터는 \tilde{\xi}라는 접공간의 가우시안 상태를 추적하며, 필요한 경우 이것을 \text{Exp}를 통해 다시 군상의 X를 보정하는 방식으로 동작합니다. 이런 접근을 흔히 오차-상태 Kalman 필터라고 하며, Lie 군 이론을 적용한 필터에서는 자연스럽게 이러한 구조가 나타나게 됩니다.

Solà 논문에서는 이러한 Lie 군 기반 필터의 절차를 유도하고, 그것이 전통적인 EKF와 거의 동일한 형태를 가짐을 보여줍니다. 우선 예측 단계를 생각해봅시다. 로봇의 상태가 시간에 따라 변화하는 모델이 주어졌다고 할 때, 만약 상태가 Lie 군 원소라면 그 상태 천이 역시 군 연산으로 표현됩니다. 예를 들어 임의의 작은 시간 \delta t 동안 상태가 변화하는 미분방정식 \dot{X}(t) = f(X(t), u(t))가 있다면, 이를 적분하여 이산화할 때 \oplus 연산을 이용한 누적곱 형태로 나타낼 수 있습니다:

X_{k+1} = X_k \oplus \tau_k = X_k \circ \text{Exp}(\tau_k), \qquad \text{여기서 } \tau_k \approx f(X_k, u_k)\,\delta t_k

즉 이전 상태 X_k에 각 시간구간의 작은 변화량 \tau_k (Lie 대수 벡터)를 지수지도를 통해 적용함으로써 다음 상태를 얻습니다. 구체적인 예로, X가 3차원 회전행렬 R이고 제어입력으로 각속도 \omega가 주어지는 경우, R_{k+1} = R_k \text{Exp}([\omega_k \delta t]*×)와 같이 예측이 이루어집니다. 이 식은 R*{k+1} = R_k (I + [\omega_k \delta t]_\times)로 1차 근사할 수 있으며, 소위 정확한 미분적분 방식을 제공하여, 유클리드 공간에서 오일러 각을 더하는 등의 근사보다 안정적이고 정확한 예측을 가능하게 합니다.

예측 단계의 공분산 전파를 위해서는 선형화(Jacobian)가 필요합니다. Lie 군에서는 상태 천이가 비선형이지만, 오차 상태 \tilde{\xi}의 관점에서는 이를 선형화할 수 있습니다. X_{k+1} = X_k \text{Exp}(\tau_k)를 X_k와 \tau_k에 대해 미소 변화시켜 Jacobian을 구하면, 이는 대략적으로 F_k = \frac{\partial (X_k \circ \text{Exp}(\tau_k))}{\partial \tilde{\xi}_k}와 같은 계산을 Lie 대수 공간에서 수행하는 것이 됩니다. 구체적인 Jacobian 계산은 다음 절에서 다루겠지만, 여기서는 결과적으로 Lie 군 기반 예측 공식이 기존 EKF의 형태와 거의 유사하게 나타난다는 점을 강조하겠습니다. 실제로 논문에서도 “이러한 Jacobian들을 사용하면 Lie 군에서의 불확실성 관리 공식이 벡터 공간에서와 매우 유사한 형태를 띤다”고 언급하고 있습니다. 이는 우리가 칼만 필터의 예측/갱신 공식을 거의 그대로 사용하되, 상태 더하기(+)를 \oplus로 바꾸고, 필요한 Jacobian 행렬들만 새롭게 계산해주면 된다는 뜻입니다. 요컨대, 틀은 동일하고 내용물만 Lie 군에 맞게 조정되는 것입니다.

다음으로 갱신 단계를 생각해보겠습니다. 로봇 센서로부터 관측된 값 z가 상태 X에 대한 어떤 함수 h(X)로 주어진다고 할 때, EKF에서는 잔차 y = z - h(\hat{x}) 및 관측 Jacobian H = \partial h/\partial x 등을 구해서 칼만 이득을 계산하고 추정값을 보정합니다. Lie 군에서도 마찬가지로, 예측 관측값 h(X_{k|k-1})와 실제 관측 z_k의 차이를 \ominus 연산으로 정의합니다. 예컨대 \tilde{y} := z_k \ominus h(X_{k|k-1}) = \text{Log}!\big(h(X_{k|k-1})^{-1} \circ z_k\big) 같은 형태로 잔차를 구할 수 있습니다. 이는 관측값이 만약 Lie 군 (예: 카메라로 본 로봇의 자세 측정이 또 하나의 Lie 군 값일 때)이라면 필요하고, 일반적인 스칼라나 벡터 관측의 경우에는 보통 \ominus를 실수 뺄셈으로 대체하면 됩니다. 핵심은 상태와 관측을 동일한 국소 좌표계로 사상하여 비교한다는 점입니다. 관측 함수의 Jacobian H도 h: G \to \mathbb{R}^m의 미분을 계산하여 구하는데, 이 역시 \frac{\partial h}{\partial X}(X) = \lim_{\tau\to0} \frac{h(X\oplus \tau) \ominus h(X)}{\tau}로 정의할 수 있습니다. 이렇게 얻은 관측 Jacobian H와 앞서의 예측 Jacobian F 등을 사용하면, 칼만 필터의 공분산 예측/갱신 공식은 기존과 동일하게 적용됩니다:

• 예측: P_{k|k-1} = F_k,P_{k-1|k-1},F_k^\top + Q_k
• 갱신: K_k = P_{k|k-1} H_k^\top (H_k P_{k|k-1} H_k^\top + R_k)^{-1},
• 상태 보정: \hat{X}*{k|k} = \hat{X}*{k|k-1} \oplus (K_k \tilde{y}_k),
• 공분산 보정: P_{k|k} = (\mathbb{I} - K_k H_k) P_{k|k-1},

여기서 Q_k, R_k는 과정 및 관측 잡음 공분산이고, K_k는 칼만 이득입니다. 위에서 상태 보정 단계에 \oplus 연산이 사용된 것에 주목하세요. 필터가 계산한 오차 상태 추정 K_k \tilde{y}_k (접공간 벡터)를 \oplus를 통해 실제 추정값에 반영함으로써, 새로운 \hat{X}는 항상 유효한 Lie 군 원소로 유지됩니다. 이처럼 Lie 군을 사용한 칼만 필터는 구조적으로는 기존 EKF와 동일하지만, 내부 연산을 Lie 군에 맞게 조정하여 곡면 위의 상태도 일관되게 추정할 수 있게 해줍니다. Solà 등은 이를 두고 “우리의 미소 Lie 이론을 활용하면 결과적으로 얻어지는 필터 공식이 표준 EKF 공식과 거의 닮은 꼴”이라고 설명합니다.

마지막으로, 이러한 방법론은 SLAM, 비주얼 오도메트리 등 다양한 모션 추정 분야에서 실용적인 가치를 입증하고 있습니다. 논문에는 몇 가지 응용 예제와 함께, 주요 Lie 군(SO(2), SO(3), SE(3), 쿼터니언 등)에 대한 수식 치트시트가 포함되어 있어, 실무자가 바로 활용할 수 있도록 했습니다. 또한 저자들은 이 이론을 구현한 C++ 라이브러리 manif를 공개하여, 개발자들이 보다 쉽게 Lie 이론 기반 필터를 적용할 수 있도록 지원하고 있습니다. 다음 절에서는 앞서 언급된 Jacobians(미분) 계산에 대해 조금 더 자세히 살펴보겠습니다.

2.4 Lie 군 위의 미분: Jacobian 계산 방법

상태 추정에서 핵심은 선형화, 즉 Jacobian 행렬을 올바르게 구하는 것입니다. Lie 군에서는 입력과 출력이 모두 곡면 위에 있으므로, 그 미분 정의를 약간 변형해야 합니다. 일반적인 다변수 함수의 Jacobian은 J = \frac{\partial f(x)}{\partial x} = \lim_{h\to0}\frac{f(x+h)-f(x)}{h}로 정의되지요. Lie 군에서는 뺄셈 대신 \ominus를 사용하면 유사한 정의를 내릴 수 있습니다. 함수 f: M \to N가 Lie 군 M의 원소를 받아 N (또 다른 Lie 군 혹은 벡터 공간)의 원소를 반환한다고 할 때, X \in M에서의 Jacobian \frac{\partial f}{\partial X}(X)를 정의하는 한 가지 방법은 아래와 같습니다:

\frac{\partial f}{\partial X}(X) ~:=~ \lim_{\tau \to 0} \frac{\,f(X \oplus \tau)\; \ominus\; f(X)\,}{\tau}\,

여기서 \tau \in T_X M는 X의 접공간에서 임의의 방향으로의 작은 변화입니다. 분자의 f(X \oplus \tau)\ominus f(X)는 f 출력 공간의 접공간에 놓인 벡터가 되며, 이를 \tau로 나누어 \tau \to 0 극한을 취하면 두 접공간 사이의 선형 사상(matrix)으로 수렴합니다. 이때 분자에서 \ominus를 취한 덕분에 f(X)의 변화량 역시 출력 공간의 국소적 선형 좌표로 표현된 점에 유의하세요. 이렇게 정의된 Jacobian은 입력 X의 국소 접공간에서 출력 f(X)의 국소 접공간으로 매핑되는 m\times n 행렬이며, 우리가 익히 아는 Jacobian 개념을 Lie 군 상황에 맞게 일반화한 것에 해당합니다.

이 정의는 개념적으로는 간단하지만, 실제 Jacobian을 계산할 때는 보통 함수 f를 이루는 기본 연산들에 대한 미분을 조합하는 방식이 더 효율적입니다. 마찬가지로 Solà 논문에서도 “역함수(Inversion), 합성(Composition), 지수(Exponentiation), 작용(Action) 등의 부분적 미분 블록을 이용하면 임의의 미분을 체인 룰로 쉽게 계산할 수 있다”고 설명합니다. 즉, Lie 군에서 자주 등장하는 기본 함수들의 Jacobian을 미리 유도해 두고, 이를 조합하면 임의의 복잡한 f의 Jacobian도 구할 수 있다는 것입니다. 예를 들어, 군의 곱 Y = X \circ U에 대해 입력 X에 대한 미분이나 U에 대한 미분, 역원 X^{-1}에 대한 미분, 로그/지수 맵에 대한 미분 등이 그러한 기본 블록들입니다. 이런 미분들을 구하는 과정에서 등장하는 것이 바로 Adjoint(아조인트)와 Left Jacobian(왼쪽 야코비안) 같은 개념입니다.

• Adjoint 행렬 \text{Ad}_X: 이는 Lie 군 G에서 특정 원소 X가 Lie 대수 공간에 갖는 작용을 나타냅니다. 직관적으로, \text{Ad}_X: \mathfrak{g} \to \mathfrak{g}는 항등원에서의 작은 움직임을 X에서의 작은 움직임으로 변환해주는 선형 사상입니다. 공식적으로는 \text{Ad}_X(\tau) = \frac{d}{d\epsilon}\big|_{\epsilon=0} X \circ \text{Exp}(\epsilon\tau)\circ X^{-1}로 정의할 수 있습니다. 실무적으로 중요한 특성은, \text{Ad}_X가 전역 접공간과 로컬 접공간 사이의 좌표 변환 행렬이라는 점입니다. 예를 들어 앞서 언급한 전역 vs 로컬 perturbation 전환에서 \delta_X = \text{Ad}_X^{-1}\delta_E라는 식으로 나타났던 바로 그 \text{Ad}가 여기에 등장합니다. \text{Ad}_X의 구체적인 형태는 Lie 군마다 다른데, 예를 들어 SE(3) (3차원 강체 변환군)의 경우 다음과 같습니다:

  \text{Ad}_{(R,t)} = \begin{pmatrix} R & -[t]_\times R \\ 0 & R \end{pmatrix} \in \mathbb{R}^{6\times6}

  여기서 X=(R,t)은 회전 R과 병진 t로 구성된 SE(3) 원소입니다. 이 행렬은 SE(3)의 Lie 대수 원소 (\rho,\theta) (병진 \rho, 회전 \theta)에 작용하여, X 좌표계에서 본 새로운 Lie 대수 값으로 변환하는 역할을 합니다. Adjoint 행렬은 군의 합성에 대한 미분을 다룰 때 유용합니다. 예를 들어 Y = X\circ U에 대해 X 쪽의 변화 \delta X가 출력 Y에 주는 영향은 U의 Adjoint를 통해 \delta Y = \delta X \circ U = \text{Ad}_U(\delta X)로 표현할 수 있습니다. 반대로 U의 변화는 \delta Y = X \circ \delta U = \text{Ad}_X(\delta U)로 나타나죠. 이처럼 Adjoint는 Lie 군의 곱셈 구조로 인한 미분적 상호작용을 선형 연산으로 옮겨주는 역할을 합니다.

• 왼쪽 Jacobian J_l (및 오른쪽 Jacobian J_r): 이는 흔히 Lie 대수에서 Lie 군으로의 지수 맵 미분에 등장하는 행렬입니다. 예를 들어 R = \text{Exp}(\theta) (SO(3)에서)라고 할 때, \theta의 작은 변화가 R에 주는 영향을 나타내는 미분이 왼쪽 Jacobian J_l(\theta)입니다. Taylor 전개 관점에서 \text{Exp}(\theta+\delta\theta) \approx \text{Exp}(\theta),J_l(\theta),\delta\theta로 정의할 수 있습니다. SO(3)의 J_l(\theta)에 대한 폐형식 해도 알려져 있으며, 다음과 같은 멱급수로 표현됩니다:

  J_l(\theta) = I - \frac{1-\cos\|\theta\|}{\|\theta\|^2}[\theta]_\times + \frac{\|\theta\| - \sin\|\theta\|}{\|\theta\|^3}[\theta]_\times^2,

  이는 \theta가 0에 가까울 때 J_l(\theta) \to I로 수렴하며, 회전 각도가 커질수록 J_l이 편차의 크기를 보정해주는 역할을 합니다. 오른쪽 Jacobian J_r(\theta)는 이와 유사하지만, \text{Exp}(\theta)R 같은 오른쪽 곱 상황의 미분에 나타나는 행렬입니다. 사실 J_r(\theta)와 J_l(\theta)는 서로 전치관계(J_r(\theta) = J_l(-\theta))에 있습니다. 이러한 Jacobian 행렬은 불확실성 전파에 중요하게 활용되는데, 예를 들어 각도 공간의 공분산을 회전행렬 공간의 공분산으로 변환할 때 P_R = J_l(\theta),P_\theta,J_l(\theta)^\top와 같이 사용됩니다. 논문의 설명에 따르면 대부분의 파생된 Jacobian은 오른쪽 미분에 기반하고, 필요한 경우 왼쪽 Jacobian도 별도로 제공하고 있습니다.

정리하면, Lie 군에서의 Jacobian 계산은 (1) 우선 각 개별 연산(Exp, Log, 곱, 역 등)의 미분 공식을 알고, (2) 체인 룰을 적용하여 복잡한 함수의 Jacobian을 구성하는 방식으로 이루어집니다. 이렇게 하면 자칫 직접 미분하면 실수하기 쉬운 부분들도 블록 조립하듯 안전하게 얻을 수 있습니다. Solà 논문 부록에는 주요 Lie 군들에 대한 거의 모든 필요한 미분 공식이 나열되어 있는데, 이는 실무자가 EKF나 최적화 알고리즘을 구현할 때 큰 도움이 됩니다. 예를 들어, h(X) = X \cdot p (Pose X가 3D 점 p에 작용) 같은 단순한 경우부터 IMU의 복잡한 상태 천이에 이르기까지, 미리 유도된 Jacobian들을 모아두면 프로토타이핑 속도와 신뢰성이 크게 향상됩니다. 실제로 Manif 라이브러리에는 이러한 Jacobian 계산이 모두 구현되어 있어, 사용자가 일일이 미분 공식을 유도할 필요 없이 함수를 호출해 사용할 수 있습니다.

참고로, Jacobian을 수기로 유도하는 작업은 매우 번거롭고 오류가 잦기 때문에, 최근에는 자동 미분이나 수치 미분을 활용하는 경우도 많습니다. 그러나 Lie 이론을 한 번 익혀 두면, 자동 미분 없이도 문제를 해석적으로 풀 수 있고 보다 깊은 이해를 얻을 수 있다는 장점이 있습니다. 논문의 저자들도 “Lie 이론을 쓰면 빠르게 최종 Jacobian을 얻을 수 있지만 수학이 많이 필요하며, 체인 룰을 직접 쓰는 편이 더 쉬울 수도 있다”는 취지의 언급을 하고 있습니다. 이는 결국 개발자가 선호하는 방식에 달렸지만, 원리를 알고 쓰는 것과 모르고 쓰는 것의 차이는 결과의 신뢰성과 확장성에서 드러날 것입니다.

2.5 유클리드 기반 필터와의 비교 – 무엇이 다르고 어떤 장점이 있나?

이제 Lie 이론 기반의 필터가 기존의 유클리드 공간 EKF 등과 어떻게 다른지, 또 어떤 장점을 갖는지 요약해보겠습니다. 핵심 차이는 당연히 상태를 다루는 방식입니다. 전통적인 필터에서는 상태를 하나의 벡터로 보고 그 위에서 + 연산을 수행합니다. 하지만 만약 상태가 본질적으로 \mathbb{R}^n가 아닌 곡면(예: 회전)은, 기존 방식은 몇 가지 문제를 일으킵니다. 아래에 Lie 군 기반 접근의 차별점과 장점을 정리했습니다.

• 상태 제약의 자연스러운 유지: Lie 군 필터에서는 상태 업데이트를 \oplus와 \text{Exp}로 수행하므로, 추정한 상태가 항상 유효한 군 원소로 유지됩니다. 예를 들어, 쿼터니언을 사용해 자세를 나타낼 때, 기존 EKF는 보정시 벡터에 \Delta q를 더한 후 재규격화(normalize)해야 하지만 Lie EKF에서는 q \leftarrow q \oplus \Delta q = q \cdot \text{Exp}(\Delta q)로 업데이트함으로써 단위 노름 조건이 자동으로 보존됩니다. 이는 구현상 실수를 줄이고, 수학적으로도 일관성(consistency)을 확보해줍니다.

• 큰 회전/변위에 대한 정확한 선형화: 유클리드 필터는 상태가 크게 변할 경우 선형화 오차가 커질 수 있습니다. 반면 Lie 이론을 사용하면, 예를 들어 90^\circ 회전도 축-각 벡터 (\pi/2)로 정확히 표현하고 지수맵으로 반영할 수 있습니다. 따라서 변화가 클 때도 오차를 적절히 반영할 수 있어 필터의 안정성이 향상됩니다. 이러한 특성 덕분에 SLAM/비주얼-관성 항법 등의 대규모 변환이 수반되는 문제에서 필터의 성능이 향상되었다는 보고가 다수 있습니다.

• 통합적인 수학적 프레임워크: Lie 군은 다양한 유형의 상태(예: 2D/3D 회전, 위치, 확장된 포즈 등)를 하나의 이론으로 아우릅니다. 기존에는 각 경우마다 좌표 표현을 달리하며 EKF 공식을 유도해야 했지만, Lie 이론을 적용하면 하나의 통일된 틀 안에서 모든 경우를 다룰 수 있습니다. Solà 논문이 제공하는 것처럼, 주요 Lie 군에 대한 공통된 연산 표기와 공식이 있으므로 학습곡선도 완만해집니다. 예를 들어, SO(2), SO(3), SE(3), \mathbb{R}^n (트리비얼 군) 등을 모두 동일한 \oplus, \ominus 표기로 다룰 수 있고, 필요한 Jacobian들도 형태는 유사한 구조를 가집니다.

• 체계적인 불확실성 전파: Lie 군 기반 필터에서는 공분산이 항상 접공간 상에 정의됩니다. 이는 곡면의 곡률을 직접 다루지 않고도 불확실성을 다룰 수 있게 해주며, 필요할 경우 접공간 상의 가우시안을 다시 군상에 랩핑(wrapping)해서 해석할 수 있습니다. 예를 들어, 아래 그림에서 빨간 타원은 접공간에서의 공분산 등고선이고, 이를 지수맵으로 곡면에 투영하면 파란 리본 모양으로 나타납니다. 이러한 시각화는 곡면 위의 불확실성 영역을 직관적으로 보여주며, 유클리드 필터에서는 얻기 어려운 통찰을 제공합니다. 더 나아가, Adjoint와 left Jacobian 등을 이용해 좌표계 변환에 따른 공분산 이식도 엄밀하게 수행할 수 있습니다. 이는 복잡한 로봇 센서 융합 시스템에서 서로 다른 표현 사이의 불확실성 변환을 일관되게 해주는 장점입니다.

• 기존 알고리듬과의 유사성 (쉬운 이식성): 앞서 설명했듯, Lie EKF의 수식은 기존 EKF와 거의 같은 형태를 띱니다. 따라서 이미 칼만 필터나 그래프 최적화 등에 익숙한 실무자라면 기존 코드를 약간 수정하는 것만으로 Lie 군 버전으로 옮길 수 있습니다. 예를 들어, Plus 연산을 지원하는 데이터 구조(쿼터니언, 변환행렬 등)를 만들고, 칼만 필터의 업데이트 부분에서 벡터 합 대신 \oplus를 호출하게 바꾸는 정도의 수정이면 됩니다. Solà 등은 “Lie 이론을 적용해도 불확실성 관리 공식이 벡터 공간의 경우와 거의 닮아 있다”고 강조하며, 독자들이 거부감 없이 기존 알고리듬을 확장하도록 돕고 있습니다.

• 이론적으로 검증된 정확성: Lie 군 필터는 근본적으로 미분 기하학에 기반하고 있어, 특이점(singularity)이나 좌표계 의존성 등의 문제가 최소화됩니다. 이는 특히 3차원 회전 같이 전통적으로 특이점 문제가 있던 경우 (예: 오일러 각의 짐벌락 문제)에도 강인합니다. 또한 시스템 모델이 좌표계 변화 아래 불변(invariant)인 성질을 이용하면, 필터의 구조적인 강건성을 높이는 Invariant-EKF와 같은 기법도 등장했는데, 이는 모두 Lie 군 이론의 산물입니다. 결과적으로 Lie 이론 기반 접근은 이론적으로 보다 철저히 검증되었고, 좌표 선택에 덜 민감한 추정을 가능케 합니다.

이와 같은 장점에도 불구하고, 실무적으로 고려해야 할 점은 구현의 복잡성 증가입니다. Lie 군을 다루려면 수치적으로 Exp/Log를 계산해야 하고, Jacobian도 새롭게 구해야 하므로 초기 구현량은 다소 늘어날 수 있습니다. 하지만 앞서 언급한 manif 라이브러리나, 이미 잘 알려진 Sophus, g2o 등의 라이브러리를 사용하면 이러한 구현 부담은 크게 줄어듭니다. 무엇보다, 한 번 Lie 이론을 도입해두면 향후 새로운 상태 변수가 추가되어도 같은 원리로 확장할 수 있고, 시스템 전반의 일관성 유지와 디버깅 용이성이 좋아지는 효과가 있습니다. Solà 등은 “필요없는 이론까지 다 동원하지 않아도, 우리에게 유용한 핵심만으로도 충분히 정확한 알고리듬을 만들 수 있다”는 메시지를 전하고 있습니다. 이는 곧 실용성과 엄밀함의 균형을 의미하며, 로봇공학자가 Lie 이론을 학습할 충분한 이유가 될 것입니다.

2.6 맺으며

지금까지 “A micro Lie theory for state estimation in robotics” 논문을 따라가며 Lie 군/대수의 기본부터 상태 추정에의 응용까지 살펴보았습니다. 요약하면, Lie 군상의 칼만 필터는 상태를 매니폴드 위에서 표현하고, 오차는 접공간에서 가우시안으로 추정하며, 업데이트는 \text{Exp}/\text{Log} 연산을 통해 이루어집니다. 이는 항상 유효한 상태를 유지하고 선형화의 정확성을 높이며, 궁극적으로 필터의 성능과 안정성을 개선합니다. 논문 저자들이 강조하듯이, 로봇 상태 추정에서 Lie 이론의 일부분만 활용해도 얻을 수 있는 이득이 매우 크다는 것이 현대 사례들로 증명되고 있습니다. 독자께서도 오래 잊고 있던 이론 감각을 되살려, 실제 로봇 문제에 Lie 이론을 적용해보길 권합니다. 작은 Lie 이론이 모여 큰 발전을 이루듯, 엄밀한 수학적 도구의 현장 적용이 로봇공학의 견고한 발전으로 이어질 것입니다.

참고문헌: Joan Solà, Jérémie Deray, Dinesh Atchuthan, A micro Lie theory for state estimation in robotics, arXiv:1812.01537v9, 2021.