📃SE(3)-Equivariant 리뷰

se3

manipulation

geometric

lie-group

survey

SE(3)-Equivariant Robot Learning and Control - A Tutorial Survey

Published

December 11, 2025

🔍 Ping. 🔔 Ring. ⛏️ Dig. A tiered review series: quick look, key ideas, deep dive.

Paper Link

✨ Equivariant neural networks는 로봇 학습에서 데이터 효율성과 일반화 능력을 향상시키기 위해 SE(3)와 같은 내재된 대칭을 아키텍처에 명시적으로 통합합니다.
📚 본 튜토리얼은 Lie 그룹 및 Lie 대수와 같은 핵심 개념을 검토하고, SE(3)-equivariant neural networks 설계(G-CNNs, steerable methods, GNNs) 및 Geometric Control을 포괄적으로 다룹니다.
🤖 이 논문은 SE(3)-equivariance를 활용한 모방 학습 및 강화 학습 애플리케이션을 소개하며, 더 강력하고 효율적인 로봇 시스템 개발을 위한 미래 방향을 제시합니다.

🔍 Ping Review

🔍 Ping — A light tap on the surface. Get the gist in seconds.

이 논문은 로봇 학습 및 제어 분야에서 SE(3)-equivariant 모델을 사용하는 최신 연구 동향을 포괄적으로 분석하고 있습니다. 기존의 딥러닝 및 Transformer 모델이 데이터의 내재된 대칭(symmetries) 및 불변성(invariances)을 처리하는 데 어려움을 겪는 반면, Equivariant Neural Networks는 이러한 속성을 아키텍처에 명시적으로 통합하여 효율성과 일반화(generalization)를 향상시킵니다. 특히, 시각 로봇 조작(visual robotic manipulation) 및 제어 설계에서 자연스러운 3D 회전 및 병진 대칭을 활용하는 SE(3)-equivariant 모델에 초점을 맞춥니다.

주요 내용 및 방법론:

SE(3) 군(Group) 및 리 대수(Lie Algebra) 기초:
- 군(Groups): 군의 정의, 부분군(subgroup), 군 작용(group action) 등을 다루며, 특히 SE(n)이 SO(n)과 병진군 R^n의 반직접곱(semidirect product)으로 정의됨을 설명합니다. SE(3)는 3D 강체 변환(rigid body transformations)을 나타냅니다.
- 행렬 리 군(Matrix Lie Groups) 및 리 대수(Lie Algebras): 리 군은 연속적이면서 미분 가능한 군으로, 리 대수는 리 군의 항등원(identity element)에서의 접 공간(tangent space)입니다. 리 대수는 리 군의 무한소 변환(infinitesimal transformations)을 나타내며, 행렬 지수 함수(matrix exponential) \exp(X)와 로그 함수(log map) \log(g)를 통해 리 군과 리 대수 간의 관계가 형성됩니다. se(3)는 SE(3)의 리 대수를 나타내며, “hat-map” (\hat{\cdot})과 “vee-map” (\check{\cdot})을 통해 벡터와 스큐-대칭 행렬(skew-symmetric matrix) 간의 사상(mapping)을 정의합니다.
- 딸림 표현(Adjoint Representation): Ad_g X = gXg^{-1}로 정의되는 리 군의 딸림 표현과 ad_X Y = [X,Y]로 정의되는 리 대수의 딸림 표현을 다룹니다. 이는 좌표계 변환을 가능하게 합니다.
- 트위스트(Twists) 및 렌치(Wrenches): se(3)의 원소는 트위스트로 불리며 공간 속도(spatial velocity) V^s = \dot{g}g^{-1}와 몸체 속도(body velocity) V^b = g^{-1}\dot{g}를 나타냅니다. 이들은 V^s = Ad_g V^b 관계를 가집니다. 렌치는 힘과 모멘트의 쌍을 나타내며, 코-딸림 작용(co-adjoint action) Ad_g^{*-1}에 의해 변환됩니다.
Equivariant Deep Learning:
- Equivariant Map: 신경망 \Phi: M \to N이 군 작용 g에 대해 G-equivariant하다는 것은 \Phi(g \circ p) = g \circ \Phi(p)를 만족하는 것을 의미합니다. 이는 입력 변환에 따라 출력이 일관되게 변환됨을 보장하여 가중치 공유(weight sharing)를 가능하게 합니다.
- 정규 군 CNN (Regular Group CNNs):
  - 표준 CNN은 병진(translation) 대칭에는 강하지만 회전(rotation) 대칭에는 취약하여 데이터 증강(data augmentation)이나 중복된 필터 학습이 필요합니다.
  - 리프팅 합성곱(Lifting Convolution): 입력 이미지를 R^2 도메인에서 군 도메인 SE(2)로 사상(map)하여 특징 맵을 생성합니다.
  - 군 합성곱(Group Convolution): SE(2) 도메인에서 직접 합성곱을 수행합니다. 하지만 연속적인 SE(2) 군에 대한 equivariance를 완전히 달성하기 위해 SE(2)를 유한 부분군 R^2 \rtimes C_N으로 이산화(discretize)하며, 이는 고차원 회전에 대한 계산 복잡성 문제를 야기합니다.
- 스티어러블 군 CNN (Steerable Group CNNs):
  - 군 CNN의 이산화 문제를 해결하기 위해 스티어러블 필터(steerable filter)를 사용합니다. 스티어러빌리티(steerability)는 함수가 군 변환에 의해 유한한 기저 함수의 선형 결합으로 표현될 수 있음을 의미합니다.
  - 구면 조화 함수(Spherical Harmonics, SH): SO(3) 변환의 기저 함수로 사용됩니다. Y_l^m(\theta, \phi)는 차수(degree) l과 차수(order) m을 가지며, SO(3)의 기약 표현(irreducible representation)인 위그너-D 행렬(Wigner-D matrices) D_l(R)을 통해 equivariant하게 변환됩니다.
  - 클렙슈-고르당 텐서곱(Clebsch-Gordan Tensor Product): 스티어러블 선형 계층(linear layer)에서 u \in V_{l_1}과 v \in V_{l_2} 같은 두 스티어러블 벡터를 새로운 스티어러블 벡터 (u \otimes_{cg} v)_l^m \in V_l로 결합하는 데 사용됩니다. 이는 스티어러블 신경망의 핵심 요소입니다.
  - SE(3)-Equivariant Graph Neural Networks: 3D 포인트 클라우드(point cloud) 데이터 처리에 사용되며, Tensor Field Networks (TFNs) 및 SE(3)-Transformers와 같은 아키텍처를 통해 SE(3)-equivariance를 달성합니다. 이는 각 포인트에 부착된 특징 벡터(feature vector)가 SE(3) 군 작용에 따라 적절히 변환되도록 합니다. Equivariant Spherical Channel Network (eSCN)은 텐서곱의 계산 복잡도를 줄이는 효율적인 대안을 제시합니다.
로보틱스에서의 Equivariant Deep Learning 응용:
- 모방 학습(Imitation Learning): Equivariant Descriptor Fields (EDFs)는 pick-and-place 문제에 대한 SE(3) bi-equivariant 에너지 기반 모델을 제안하여 높은 샘플 효율성과 아웃-오브-분포(out-of-distribution) 데이터에 대한 강건성(robustness)을 달성합니다. 이는 장면(scene)과 잡기(grasp) 모두에 대한 equivariance를 고려합니다. Diffusion-EDFs는 이를 확산 모델(diffusion models)과 결합하여 훈련 시간을 개선합니다. Fourier Transporter는 3D 합성곱과 푸리에 표현(Fourier representation)을 사용하여 SE(3) bi-equivariant 모델을 제안합니다.
- 강화 학습(Reinforcement Learning): 군-불변 마르코프 결정 과정(Group-Invariant Markov Decision Process, MDP) 개념을 기반으로 합니다. 이 프레임워크는 보상 함수(reward function) R(s, a) = R(g \circ s, g \circ a) 및 전이 확률(transition probability) P(s'|s, a) = P(g \circ s'|g \circ s, g \circ a)이 군-불변(group-invariant)일 때 최적 Q 함수(Q function) Q^*(s, a)가 군-불변이 되고 최적 정책(policy) \pi^*(s)이 equivariant하게 \pi^*(g \circ s) = g \circ \pi^*(s) 됨을 증명합니다. 이를 통해 샘플 효율성과 일반화 능력을 향상시킵니다.
기하학적 임피던스 제어 (Geometric Impedance Control):
- 로봇 매니퓰레이터(manipulator)의 작업 공간(workspace) 역학을 SE(3) 구조를 사용하여 정의합니다.
- 오차 함수(Error Functions): SE(3) 상의 두 지점 간의 “거리”를 나타내는 스칼라 값으로, 행렬 군(matrix group) 관점 (\Psi_1(g, g_d) = \frac{1}{2} \|I - g_d^T g\|_F^2)과 리 대수(Lie algebra) 관점 (\Psi_2(g, g_d) = \frac{1}{2} \|\xi_{de}\|^2_K)에서 오차 함수를 정의합니다.
- 위치 오차 벡터(Positional Error Vector) 및 속도 오차 벡터(Velocity Error Vector): Lie 군 기반 오차 함수로부터 Geometrically Consistent Error Vector (GCEV) e_G를 도출하고, 다른 접 공간(tangent spaces)에 있는 두 접 벡터(tangent vectors)를 비교하기 위해 속도 오차 벡터 e_V를 정의합니다.
- 에너지 함수(Energy Functions): 위치 오차 함수를 기반으로 퍼텐셜 에너지 함수(potential energy function) P_i(g, g_d)를 정의하고, 속도 오차 벡터와 관성 행렬(inertia matrix)을 사용하여 운동 에너지(kinetic energy) K(t,q,\dot{q})를 정의합니다.
- SE(3)-Equivariant 제어 법칙: GIC는 총 기계 에너지(total mechanical energy)가 시간에 따라 소멸되도록 설계된 제어 법칙입니다. 특히, GIC는 공간 좌표계(spatial frame)에서 기술될 때 SE(3)-equivariant함을 보입니다. 이는 피드백 항(feedback terms) f_G가 좌불변(left-invariant) 속성 f_G(g_l g, g_l g_d) = f_G(g, g_d)을 가지기 때문입니다.

향후 연구 방향:

비전-대-힘 SE(3)-Equivariance (Vision-to-Force SE(3)-Equivariance): 시각 정보뿐만 아니라 힘 상호작용(force interaction)을 포함하는 조작 작업에서 equivariance를 통합하여 샘플 효율성을 높이는 연구.
로보틱스 및 시스템에서의 대칭 깨짐(Symmetry Breaking): 로봇의 특이점(singular configuration)이나 제어 시스템의 제약(constraints)과 같은 요인으로 인해 발생하는 대칭 깨짐 현상과, 관측 공간(observation space)의 불완전성(imperfection)이 equivariant 네트워크 성능에 미치는 영향에 대한 연구.

이 논문은 로봇 조작 및 제어 분야에서 equivariant 딥러닝과 기하학적 제어의 융합을 위한 포괄적인 이론적 틀과 실용적 적용 사례를 제시하고 있습니다.

🔔 Ring Review

🔔 Ring — An idea that echoes. Grasp the core and its value.

“자연의 법칙은 아름답고, 그 아름다움의 핵심에는 대칭성이 있다.”
— 리처드 파인만

1장: 대칭성이란 무엇인가?

🪞 거울 앞에서 생각해보기

먼저 질문 하나 던져볼게. 네가 거울 앞에 서 있다고 상상해봐. 너는 오른손을 들었는데, 거울 속 너는 왼손을 들고 있지? 이게 바로 “거울 대칭”이야.

자, 이번엔 다른 걸 생각해보자. 네 방에 컵이 하나 있어. 이 컵을:

회전시켜도 (돌려도) — 여전히 같은 컵이야
이동시켜도 (책상에서 바닥으로 옮겨도) — 여전히 같은 컵이야

이렇게 어떤 변환을 해도 본질이 변하지 않는 성질, 그게 바로 대칭성(Symmetry)이야.

🌍 왜 이게 로봇에게 중요할까?

로봇 팔이 컵을 집으려고 한다고 생각해봐. 컵이 책상 왼쪽에 있든, 오른쪽에 있든, 45도 돌아가 있든 — 컵을 집는 방법의 본질은 똑같아야 하지 않겠어?

문제는 기존의 인공지능(딥러닝)은 이걸 잘 모른다는 거야. 컵이 정면에 있을 때 집는 법을 배웠는데, 컵을 90도 돌려놓으면 “어? 이건 뭐지?” 하고 당황해버려.

해결책: 대칭성을 처음부터 신경망 구조에 넣어버리면 어떨까?

2장: 군(群, Group)이란 무엇인가?

🎮 변환들의 게임

“군”이라는 단어가 좀 무섭지? 근데 사실 엄청 단순한 아이디어야.

군(Group)이란 “변환들의 모임”인데, 특별한 규칙 네 가지를 만족해야 해:

규칙 1: 닫힘 (Closure)

두 변환을 연속으로 하면, 그 결과도 같은 종류의 변환이어야 해.

예를 들어, 시계 방향 30도 회전 후에 시계 방향 60도 회전을 하면? 시계 방향 90도 회전이지! 여전히 “회전”이야.

수학으로 쓰면:

g_1 \cdot g_2 \in G \quad \text{(두 원소의 결합도 그 군에 속함)}

규칙 2: 결합법칙 (Associativity)

세 개의 변환 g_1, g_2, g_3이 있을 때:

(g_1 \cdot g_2) \cdot g_3 = g_1 \cdot (g_2 \cdot g_3)

어떤 순서로 괄호를 묶어도 결과가 같아. 마치 (2 \times 3) \times 4 = 2 \times (3 \times 4)인 것처럼!

규칙 3: 항등원 (Identity)

“아무것도 안 하는” 변환이 있어야 해. 이걸 e 또는 1이라고 불러.

g \cdot e = e \cdot g = g

0도 회전 = 회전 안 함 = 원래 그대로!

규칙 4: 역원 (Inverse)

모든 변환에는 “되돌리는” 변환이 있어야 해.

g \cdot g^{-1} = g^{-1} \cdot g = e

시계 방향 30도 회전의 역원? 반시계 방향 30도 회전이지!

📦 실제 예시들

군의 이름	뭘 하는 변환인가	수학 기호
평행이동군	공간에서 이동	(\mathbb{R}^n, +)
회전군	3D 회전	SO(3)
특수 유클리드 군	회전 + 이동	SE(3)
일반선형군	뒤집을 수 있는 행렬들	GL(n)

3장: SO(3)와 SE(3) — 우리가 사는 3차원 세계

🔄 SO(3): 3차원 회전의 세계

SO(3)은 “Special Orthogonal group in 3 dimensions”의 약자야. 무슨 말이냐면:

3차원 공간에서 가능한 모든 회전

“Special”의 의미는 “뒤집기(reflection) 없이 순수한 회전만”이라는 뜻이야.

SO(3)의 회전은 3×3 회전 행렬 R로 표현할 수 있어:

R \in SO(3) \iff R^T R = I \text{ 그리고 } \det(R) = 1

여기서: - R^T는 R의 전치행렬 (행과 열을 바꾼 것) - I는 단위행렬 (대각선만 1, 나머지 0) - \det(R) = 1은 “크기를 변형하지 않고, 뒤집지도 않는다”는 뜻

왜 R^T R = I일까?

회전 행렬의 각 열(또는 행)은 직교하는 단위벡터들이야. 서로 수직이고, 길이가 1이라는 거지. 이 조건을 수학으로 쓰면 R^T R = I가 돼.

🚶 SE(3): 회전 + 이동의 세계

SE(3)은 “Special Euclidean group in 3 dimensions”의 약자야:

3차원 공간에서 가능한 모든 회전과 평행이동의 조합

이건 4×4 행렬로 표현할 수 있어:

T = \begin{bmatrix} R & p \\ 0 & 1 \end{bmatrix} \in SE(3)

여기서: - R: 3×3 회전 행렬 (SO(3)의 원소) - p: 3×1 평행이동 벡터 (어디로 이동할지) - 마지막 행 [0, 0, 0, 1]은 계산을 편하게 하기 위한 트릭이야

실제 변환은 어떻게 계산할까?

3D 점 x = (x_1, x_2, x_3)에 SE(3) 변환을 적용하면:

\begin{bmatrix} x' \\ 1 \end{bmatrix} = \begin{bmatrix} R & p \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ 1 \end{bmatrix} = \begin{bmatrix} Rx + p \\ 1 \end{bmatrix}

즉, 먼저 회전(Rx)하고, 그 다음 이동(+p)하는 거야!

🤔 왜 SE(3)가 로봇에게 중요할까?

로봇이 사는 세계를 생각해봐:

카메라로 물체를 볼 때 — 카메라 위치와 각도에 따라 보이는 게 달라
팔로 물건을 집을 때 — 물건의 위치와 방향에 따라 접근 방법이 달라
이동할 때 — 출발점에서 목적지까지 회전하고 이동해야 해

이 모든 게 SE(3) 변환이야!

4장: 등변성(Equivariance)과 불변성(Invariance)

🎯 핵심 개념: 변환에 어떻게 반응하는가?

자, 이제 오늘의 주인공을 소개할게: 등변성(Equivariance)

함수 f가 있고, 입력 x에 변환 g를 적용한다고 해보자.

불변성 (Invariance)

출력이 변하지 않으면 불변(Invariant)이야:

f(g \cdot x) = f(x)

예시: 물체 인식. 컵을 돌려도 “이건 컵이다”라는 판단은 변하지 않아야 해.

등변성 (Equivariance)

출력이 입력과 같은 방식으로 변하면 등변(Equivariant)이야:

f(g \cdot x) = g \cdot f(x)

예시: 물체 위치 찾기. 컵을 오른쪽으로 10cm 옮기면, “컵의 위치”라는 출력도 오른쪽으로 10cm 옮겨져야 해.

🖼️ 그림으로 이해하기

삼각형의 무게중심(centroid)을 구하는 함수를 생각해봐:

원래 삼각형        →    함수 f    →    무게중심 점
     △                                    •

  (회전 적용)                          (같은 회전 적용)
     ↓                                    ↓

회전된 삼각형      →    함수 f    →    회전된 무게중심
     △                                    •

삼각형을 돌리고 나서 무게중심을 구하든, 무게중심을 구하고 나서 그 점을 돌리든, 결과가 같아야 해. 이게 바로 등변성이야!

📐 수학적으로 더 정확하게

입력 공간 X와 출력 공간 Y가 있고, 군 G가 두 공간에 각각 작용한다고 해보자: - G가 X에 작용하는 방식: \rho_X(g) - G가 Y에 작용하는 방식: \rho_Y(g)

함수 f: X \to Y가 G-등변이려면:

f(\rho_X(g) \cdot x) = \rho_Y(g) \cdot f(x), \quad \forall g \in G, \forall x \in X

불변성은 등변성의 특수한 경우야. \rho_Y(g)가 항상 항등 변환일 때:

f(\rho_X(g) \cdot x) = f(x)

5장: 리 군(Lie Group)과 리 대수(Lie Algebra)

🌊 연속적인 변환의 세계

지금까지 배운 군 중에서 SO(3)와 SE(3)는 특별해. 왜냐하면 변환이 연속적이거든.

정육면체를 90도씩만 돌릴 수 있는 게 아니라, 1도, 0.001도, 아무 각도로나 돌릴 수 있잖아? 이렇게 연속적으로 변할 수 있는 군을 리 군(Lie Group)이라고 불러.

리 군 = 군 + 미분 가능한 매끄러운 구조

🧮 리 대수: 변화의 “속도”

리 대수는 좀 추상적인데, 직관적으로 설명해볼게.

리 군이 “어디에 있는가”라면,
리 대수는 “어느 방향으로 얼마나 빨리 변하는가”야.

수학적으로, 리 대수 \mathfrak{g}는 항등원 근처에서의 접선 공간이야:

\mathfrak{g} = T_e G

🔄 SO(3)의 리 대수: \mathfrak{so}(3)

SO(3)의 리 대수는 반대칭 행렬(skew-symmetric matrix)들의 집합이야:

\mathfrak{so}(3) = \{\Omega \in \mathbb{R}^{3 \times 3} : \Omega^T = -\Omega\}

반대칭 행렬이 뭐냐면:

\Omega = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix}

이건 3차원 벡터 \omega = (\omega_1, \omega_2, \omega_3)와 일대일 대응돼. 이 벡터가 바로 각속도 벡터야!

Hat 연산자와 Vee 연산자

벡터를 반대칭 행렬로 바꾸는 걸 Hat 연산자 (\cdot)^\wedge라고 해:

\omega^\wedge = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix}

반대로 행렬을 벡터로 바꾸는 건 Vee 연산자 (\cdot)^\vee:

(\omega^\wedge)^\vee = \omega

🌉 지수 사상: 리 대수에서 리 군으로

리 대수(속도)에서 리 군(위치)으로 가는 다리가 있어. 이걸 지수 사상(Exponential Map)이라고 불러:

\exp: \mathfrak{g} \to G

SO(3)의 경우, 유명한 로드리게스 공식(Rodrigues’ Formula)을 써:

\exp(\omega^\wedge) = I + \frac{\sin\theta}{\theta}\omega^\wedge + \frac{1 - \cos\theta}{\theta^2}(\omega^\wedge)^2

여기서 \theta = \|\omega\|는 회전 각도야.

직관적 의미: 각속도 \omega로 1초 동안 회전하면 어디에 도착하는가?

🔄 SE(3)의 리 대수: \mathfrak{se}(3)

SE(3)의 리 대수는 이렇게 생겼어:

\xi^\wedge = \begin{bmatrix} \omega^\wedge & v \\ 0 & 0 \end{bmatrix} \in \mathfrak{se}(3)

여기서: - \omega \in \mathbb{R}^3: 각속도 (회전 방향과 속도) - v \in \mathbb{R}^3: 선속도 (이동 방향과 속도)

6차원 벡터 \xi = (v, \omega)로 표현하기도 해. 이걸 트위스트(twist)라고 불러.

6장: 등변 신경망의 설계

🧠 왜 일반 신경망은 대칭성을 이해 못할까?

일반적인 신경망(MLP, CNN 등)은 입력 데이터의 대칭성을 모르고 무식하게 학습해.

예를 들어, 컵 이미지로 “컵 인식”을 학습했는데: - 컵이 정면에 있을 때: 잘 인식! ✓ - 컵을 45도 돌리면: “이건 뭐지…?” ✗ - 컵을 뒤집으면: “완전 모르겠어!” ✗

해결책 1: 데이터 증강(Data Augmentation). 온갖 각도의 컵 이미지를 다 보여줘!

문제: 데이터가 엄청 많이 필요하고, 시간도 오래 걸려.

해결책 2: 등변 신경망. 처음부터 대칭성을 아는 구조를 만들어!

🔧 등변 신경망의 핵심 아이디어

등변 신경망은 각 층(layer)이 등변 함수가 되도록 설계해:

\text{Layer}_i(g \cdot x) = g \cdot \text{Layer}_i(x)

신기한 건, 등변 층을 연속으로 쌓으면 전체 네트워크도 등변이 된다는 거야!

f = \text{Layer}_n \circ \cdots \circ \text{Layer}_2 \circ \text{Layer}_1

각 층이 등변이면:

f(g \cdot x) = \text{Layer}_n(\cdots(\text{Layer}_1(g \cdot x))) = g \cdot \text{Layer}_n(\cdots(\text{Layer}_1(x))) = g \cdot f(x)

📊 포인트 클라우드와 SE(3)-등변성

로봇 시각에서 많이 쓰는 데이터 형태가 포인트 클라우드(Point Cloud)야. 3D 공간의 점들 집합이지:

X = \{x_1, x_2, \ldots, x_N\}, \quad x_i \in \mathbb{R}^3

SE(3) 변환 T = (R, p)를 적용하면:

T \cdot X = \{Rx_1 + p, Rx_2 + p, \ldots, Rx_N + p\}

SE(3)-등변 신경망은 이런 성질을 만족해:

f(T \cdot X) = T \cdot f(X)

포인트 클라우드를 돌리거나 옮겨도, 출력도 똑같이 돌아가거나 옮겨져야 해!

🔬 텐서장 신경망 (Tensor Field Networks)

등변 신경망의 대표적인 예가 텐서장 신경망(TFN)이야.

핵심 아이디어: 각 점에 스칼라, 벡터, 고차 텐서 특성을 붙이고, 이것들이 변환에 따라 적절히 변하도록 해.

텐서 종류	차수 l	성분 수	회전에 대한 반응
스칼라	0	1	변하지 않음
벡터	1	3	회전 행렬로 변환
행렬	2	5 (traceless)	더 복잡한 변환

회전에 대한 반응은 비가약 표현(Irreducible Representation)으로 기술해:

D^{(l)}(R) \in \mathbb{R}^{(2l+1) \times (2l+1)}

차수 l인 특성 f^{(l)}는 회전 R에 의해 이렇게 변환돼:

f^{(l)} \mapsto D^{(l)}(R) \cdot f^{(l)}

🔗 메시지 패싱과 등변성

그래프 신경망에서 자주 쓰는 메시지 패싱(Message Passing)도 등변하게 만들 수 있어:

h_i' = \phi\left(h_i, \sum_{j \in \mathcal{N}(i)} \psi(h_i, h_j, e_{ij})\right)

여기서: - h_i: 노드 i의 특성 - \mathcal{N}(i): i의 이웃 노드들 - e_{ij}: 간선 특성 (예: 두 점 사이의 거리) - \phi, \psi: 등변 함수들

핵심: 거리 \|x_i - x_j\|는 SE(3)-불변이야! 회전하거나 이동해도 두 점 사이 거리는 변하지 않으니까.

7장: 로봇 학습에의 응용

🎓 모방 학습 (Imitation Learning)

사람이 로봇에게 시범을 보여주면, 로봇이 그걸 따라 하는 거야.

문제: 시범을 보인 위치랑 실제 작업 위치가 다르면?

기존 방법: 수많은 다른 위치에서 시범을 보여줘야 해.

SE(3)-등변 방법: 하나의 시범만으로도, 다른 위치와 각도에 자동으로 일반화해!

수학적으로, 정책(policy) \pi가 등변이면:

\pi(g \cdot s) = g \cdot \pi(s)

상태 s를 변환하면, 행동도 같은 방식으로 변환돼.

🎮 강화 학습 (Reinforcement Learning)

로봇이 시행착오를 통해 스스로 배우는 방법이야.

문제: 샘플 효율이 너무 낮아. 수백만 번 시도해야 겨우 배워.

SE(3)-등변 방법: 하나의 경험에서 대칭성을 이용해 여러 경험을 “공짜로” 얻을 수 있어!

예를 들어, 컵을 특정 각도에서 집는 법을 배웠다면, 대칭성을 이용해 다른 모든 각도에서 집는 법도 자동으로 아는 거야.

수학적으로, Q-함수가 불변이면:

Q(g \cdot s, g \cdot a) = Q(s, a)

상태와 행동을 같이 변환해도 가치는 변하지 않아.

🛠️ 실제 응용 예시

1. 물체 집기 (Grasping)

입력: 물체의 포인트 클라우드
출력: 집는 위치와 방향 (SE(3) 변환!)
등변 요구사항: 물체를 돌리면, 집는 자세도 같이 돌아야 해

2. 궤적 계획 (Trajectory Planning)

입력: 시작 자세, 목표 자세
출력: 경로 (SE(3) 변환들의 시퀀스)
등변 요구사항: 전체 문제를 변환하면, 해답 경로도 같이 변환

3. 힘 제어 (Force Control)

로봇이 표면을 따라 일정한 힘을 유지하며 이동
좌표계가 바뀌어도 제어 법칙은 동일하게 작동해야 해

8장: 기하학적 제어와 SE(3)

🎯 왜 기하학적 제어가 필요할까?

전통적인 제어 이론은 주로 유클리드 공간 \mathbb{R}^n에서 동작해. 하지만 로봇의 자세(pose)는 \mathbb{R}^n이 아니라 SE(3) 위의 점이야.

예를 들어, 두 회전 사이의 “평균”을 어떻게 구할까? 단순히 행렬을 더해서 2로 나누면 안 돼 — 결과가 회전 행렬이 아닐 수 있거든!

기하학적 제어는 SE(3)의 구조를 존중하면서 제어 법칙을 설계하는 거야.

📏 오차 함수의 정의

두 SE(3) 자세 T_1, T_2 사이의 오차를 어떻게 정의할까?

상대 변환을 사용해:

T_e = T_1^{-1} T_2

이건 “첫 번째 자세에서 두 번째 자세로 가려면 어떤 변환이 필요한가?”를 나타내.

리 대수로 변환하면:

\xi_e = \log(T_e)^\vee \in \mathbb{R}^6

이 6차원 벡터가 바로 자세 오차야.

⚙️ PD 제어기의 기하학적 버전

유클리드 공간에서의 PD 제어기:

u = -K_p e - K_d \dot{e}

SE(3)에서의 기하학적 버전:

u = -K_p \xi_e - K_d \dot{\xi}_e

여기서 \xi_e는 위에서 정의한 자세 오차야.

이 제어기는 SE(3)-등변이야:

u(g \cdot T, g \cdot T_d) = g \cdot u(T, T_d)

좌표계를 바꿔도 제어 법칙이 일관성 있게 작동한다는 뜻이지!

9장: 수식 총정리

핵심 정의들

1. 군 (Group) (G, \cdot)

\begin{align} &\text{닫힘:} \quad g_1 \cdot g_2 \in G \\ &\text{결합법칙:} \quad (g_1 \cdot g_2) \cdot g_3 = g_1 \cdot (g_2 \cdot g_3) \\ &\text{항등원:} \quad \exists e : g \cdot e = e \cdot g = g \\ &\text{역원:} \quad \forall g, \exists g^{-1} : g \cdot g^{-1} = e \end{align}

2. SO(3) — 3D 회전군

SO(3) = \{R \in \mathbb{R}^{3 \times 3} : R^T R = I, \det(R) = 1\}

3. SE(3) — 특수 유클리드 군

SE(3) = \left\{ T = \begin{bmatrix} R & p \\ 0 & 1 \end{bmatrix} : R \in SO(3), p \in \mathbb{R}^3 \right\}

4. 등변성 (Equivariance)

f(\rho_X(g) \cdot x) = \rho_Y(g) \cdot f(x), \quad \forall g \in G

5. 불변성 (Invariance)

f(g \cdot x) = f(x), \quad \forall g \in G

6. 리 대수 \mathfrak{so}(3)

\omega^\wedge = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix}, \quad \omega \in \mathbb{R}^3

7. 리 대수 \mathfrak{se}(3)

\xi^\wedge = \begin{bmatrix} \omega^\wedge & v \\ 0 & 0 \end{bmatrix}, \quad \xi = \begin{bmatrix} v \\ \omega \end{bmatrix} \in \mathbb{R}^6

8. 지수 사상 (로드리게스 공식)

\exp(\omega^\wedge) = I + \frac{\sin\theta}{\theta}\omega^\wedge + \frac{1-\cos\theta}{\theta^2}(\omega^\wedge)^2, \quad \theta = \|\omega\|

10장: 마무리 — 왜 이게 중요할까?

🚀 등변 신경망의 장점

샘플 효율: 적은 데이터로 더 빨리 학습
일반화: 본 적 없는 자세나 위치에도 잘 작동
물리적 일관성: 자연의 대칭성을 존중
해석 가능성: 왜 그런 결정을 내렸는지 이해하기 쉬움

“자연은 단순함을 좋아해. 만약 네 이론이 너무 복잡하다면, 아마 뭔가 빠뜨린 거야.”

SE(3)-등변성이 복잡해 보일 수 있지만, 사실 이건 자연의 단순함을 존중하는 것이야.

물체를 돌리면 집는 자세도 돌아야 하는 건 당연한 거잖아? 등변 신경망은 이 “당연함”을 수학으로 표현한 것뿐이야.

로봇이 세상을 우리처럼 자연스럽게 이해하려면, 이런 기본적인 대칭성을 알아야 해. 그리고 이제 너도 그 비밀을 알게 됐어!

📚 더 공부하고 싶다면

군론 기초: “Group Theory in a Nutshell for Physicists” — Anthony Zee
기하학적 딥러닝: “Geometric Deep Learning” — Bronstein et al.
로봇 역학: “A Mathematical Introduction to Robotic Manipulation” — Murray, Li, Sastry
이 논문 원본: Seo et al., “SE(3)-Equivariant Robot Learning and Control: A Tutorial Survey” (arXiv:2503.09829)

⛏️ Dig Review

⛏️ Dig — Go deep, uncover the layers. Dive into technical detail.

1. 서론 (Introduction)

1.1 배경: 딥러닝과 로보틱스의 만남

최근 딥러닝의 발전은 로보틱스 분야에 혁명적인 변화를 가져왔다. 모방 학습(Imitation Learning), 강화 학습(Reinforcement Learning), 그리고 대규모 언어 모델(LLM) 기반의 멀티모달 인식 및 의사결정 기술이 로봇이 복잡한 환경을 이해하고 적응하는 데 크게 기여하고 있다.

1.2 문제점: 기존 딥러닝의 한계

하지만 기존의 딥러닝과 트랜스포머 모델에는 근본적인 문제가 있다:

대칭성(Symmetry)과 불변성(Invariance)을 본질적으로 다루지 못함
이를 보완하기 위해 대규모 데이터셋이나 광범위한 데이터 증강(Data Augmentation)이 필요함
결과적으로 학습 효율이 떨어지고, 일반화 성능도 제한적임

1.3 해결책: 등변 신경망 (Equivariant Neural Networks)

등변 신경망은 대칭성과 불변성을 신경망 구조 자체에 명시적으로 통합함으로써 이러한 한계를 극복한다. 특히 SE(3)-등변 모델은 3D 공간에서의 회전과 평행이동 대칭성을 활용하여 시각 기반 로봇 조작(Visual Robotic Manipulation)에서 뛰어난 효율성과 일반화 성능을 보인다.

1.4 논문의 기여

이 서베이 논문의 주요 기여는 다음과 같다:

그룹 등변 딥러닝과 제어에 대한 포괄적인 리뷰
그룹 등변 딥러닝의 수학적 개념과 구조에 대한 심층적인 설명
기하학적 제어(Geometric Control) 관점에서의 그룹 등변 제어 방법론 리뷰
로보틱스 분야에서 혼용되는 표기법들을 통일된 수학적 표기법으로 정리

2. 사전 지식 (Preliminaries)

이 섹션에서는 기하학적 딥러닝과 제어를 이해하기 위한 수학적 기초를 다룬다. 특히 SE(3)는 강체 변환(Rigid Body Transformation)을 분석하고 로보틱스의 다양한 비전 및 조작 작업에 필수적인 개념이다.

2.1 군 (Groups)

2.1.1 군의 정의

군(Group) (G, \cdot)은 집합 G와 이항 연산 “\cdot”로 구성되며, 다음 네 가지 공리를 만족해야 한다:

공리	수학적 표현	설명
닫힘 (Closure)	\forall h, g \in G \Rightarrow h \cdot g \in G	두 원소의 연산 결과도 군에 속함
항등원 (Identity)	\exists 1 \in G : 1 \cdot g = g \cdot 1 = g	연산해도 변하지 않는 원소 존재
역원 (Inverse)	\forall g \in G, \exists g^{-1} : g^{-1} \cdot g = g \cdot g^{-1} = 1	모든 원소에 역원 존재
결합법칙 (Associativity)	(g \cdot h) \cdot f = g \cdot (h \cdot f)	연산 순서 괄호 위치 무관

2.1.2 군의 예시

평행이동군 (Translation Group) (\mathbb{R}^n, +): - 집합: \mathbb{R}^n의 벡터들 - 연산: 벡터 덧셈, x_1 \cdot x_2 = x_1 + x_2 - 항등원: 1 = 0 (원점) - 역원: g^{-1} = -g

일반선형군 (General Linear Group) GL(n, \mathbb{R}): - 집합: 역행렬이 존재하는 n \times n 실수 행렬들

GL(n, \mathbb{R}) := \{A \in \mathbb{R}^{n \times n} | \det(A) \neq 0\}

연산: 행렬 곱셈
항등원: 단위 행렬 I_n
역원: 역행렬 A^{-1}

2.1.3 부분군 (Subgroup)

부분군은 같은 연산 하에서 군 자체가 되는 군의 부분집합 (H \subset G)이다.

중요한 부분군들:

군	정의	설명
GL^+(n, \mathbb{R})	\{A \in \mathbb{R}^{n \times n} \\| \det(A) > 0\}	양의 행렬식을 가진 행렬
U(n)	\{A \in \mathbb{C}^{n \times n} \\| AA^* = I\}	유니터리 군
O(n)	\{A \in \mathbb{R}^{n \times n} \\| AA^T = I\}	직교 군
SO(n)	\{R \in \mathbb{R}^{n \times n} \\| R^TR = RR^T = I, \det(R) = +1\}	특수 직교 군 (회전 행렬)

2.1.4 군 작용 (Group Actions)

군 G가 집합 M에 작용한다는 것은 다음을 만족하는 사상 G \times M \to M이 존재한다는 것이다.

좌작용 (Left Action): g_1 \circ (g_2 \circ p) = (g_1 \cdot g_2) \circ p, \quad e \circ p = p, \quad \forall g_1, g_2 \in G, p \in M

우작용 (Right Action): (p \circ g_1) \circ g_2 = p \circ (g_1 \cdot g_2), \quad p \circ e = p

예시: 3차원 벡터에 대한 회전 작용 SO(3) \times \mathbb{R}^3 \to \mathbb{R}^3, \quad (R, p) \to R \circ p = Rp

2.1.5 반직접곱 (Semidirect Product)

두 군 H와 N이 있고, H가 N에 좌작용 \theta_h : H \times N \to N을 한다면, 반직접곱 N \rtimes H를 정의할 수 있다:

(n, h) \cdot (n', h') = (n \cdot \theta_h(n'), h \cdot h') = (n \cdot (h \circ n'), h \cdot h')

2.1.6 특수 유클리드 군 SE(3)

SE(3)는 모든 강체 변환(평행이동과 회전)으로 구성된 군으로, 회전-평행이동 군이라고도 불린다.

SE(n) = \mathbb{R}^n \rtimes SO(n)

군 연산: g_1 \cdot g_2 = (p_1 + R_1 p_2, R_1 R_2)

역원: g^{-1} = (-R^{-1}p, R^{-1})

여기서 g_1 = (p_1, R_1), g_2 = (p_2, R_2)는 SE(n)의 원소이다.

2.2 행렬 리 군과 리 대수 (Matrix Lie Groups and Algebras)

2.2.1 리 군 (Lie Groups)

리 군은 연속군이면서 동시에 미분 가능한 다양체(Manifold)인 군이다. 즉, 군 구조와 매끄러운 기하학적 구조를 동시에 가진다.

리 군의 예시:

평행이동군 (\mathbb{R}^n, +)
일반선형군 GL(n, \mathbb{R})
회전군 SO(n)
특수 유클리드 군 SE(n)

행렬 리 군은 각 원소 g \in G가 n \times n 행렬이고, 군 연산이 행렬 곱셈이며, 곱셈과 역변환이 모두 해석적(analytic)인 군이다.

2.2.2 리 대수 (Lie Algebras)

단위 행렬 I_n에 매우 가까운 군 원소를 생각해보자:

g(\varepsilon) = I_n + \varepsilon X, \quad |\varepsilon| \ll 1

여기서 X \in \mathfrak{g} = T_{I_n}G는 생성자(Generator)라 불리며, \mathfrak{g}는 G의 항등원에서의 접선 공간(Tangent Space)으로 리 대수라고 불린다.

SO(2)의 리 대수 예시:

SO(2)의 회전 행렬: R_\theta = R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}

항등원 근처에서의 섭동: R(\varepsilon) \approx I_2 + \varepsilon \frac{\partial R(\theta)}{\partial \theta}\bigg|_{\theta=0} = I_2 + \varepsilon X

생성자: X = \frac{\partial R(\theta)}{\partial \theta}\bigg|_{\theta=0} = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}

따라서 \mathfrak{so}(2) = \{A \in \mathbb{R}^{2 \times 2} | A^T = -A\}, 즉 모든 2 \times 2 반대칭 행렬의 집합이다.

2.2.3 지수 사상 (Exponential Map)

무한소 변환 R(\varepsilon) = I_2 + \varepsilon X를 무한히 많이 곱하면 유한 변환을 얻는다:

R(\theta) = \lim_{N \to \infty} \left(I_2 + \frac{\theta}{N}X\right)^N = \exp(X\theta)

일반적인 행렬 리 군에서, 리 대수 원소 X \in \mathfrak{g}와 t \in \mathbb{R}에 대해:

g(t) = \exp(tX) = \sum_{n=0}^{\infty} \frac{1}{n!}(tX)^n

중요한 성질: \frac{d}{dt}\exp(tX)\bigg|_{t=0} = X

로그 사상 (Log Map): 지수 사상의 역함수 \log : G \to \mathfrak{g}, \quad \text{if } g = \exp(X), \text{ then } X = \log(g)

2.2.4 Hat-map과 Vee-map

리 대수 \mathfrak{g}가 l차원 벡터 공간일 때:

Hat-map \widehat{(\cdot)} : \mathbb{R}^l \to \mathfrak{g}: 벡터를 리 대수 원소로 변환

Vee-map (\cdot)^\vee : \mathfrak{g} \to \mathbb{R}^l: 리 대수 원소를 벡터로 변환

2.2.5 리 괄호 (Lie Bracket)

리 대수 \mathfrak{g}는 리 괄호 연산 [\cdot, \cdot] : \mathfrak{g} \times \mathfrak{g} \to \mathfrak{g}를 갖추며, 다음을 만족한다:

쌍선형 (Bilinear)
반대칭 (Antisymmetric): [a, b] = -[b, a]
야코비 항등식 (Jacobi identity): [a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0

리 괄호는 비가환성의 무한소 측정으로 해석할 수 있다.

\mathfrak{so}(3)의 기저 벡터:

L_x = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix}, \quad L_y = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{bmatrix}, \quad L_z = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}

리 괄호 관계: [L_x, L_y] = L_z (및 순환 치환)

물리적 의미: x축 회전 후 y축 회전과 그 역순의 차이는 z축 주위의 작은 회전이다.

2.2.6 군 표현 (Group Representation)

정의: 리 군 G의 표현은 다음을 만족하는 사상 D : G \to GL(V)이다:

D(g)D(h) = D(g \cdot h), \quad \forall g, h \in G

동치 표현 (Equivalent Representations): 기저 변환 U가 존재하여: D'(g) = UD(g)U^{-1}, \quad \forall g \in G

기약 표현 (Irreducible Representation): 더 이상 작은 부분공간으로 분해(블록 대각화)할 수 없는 표현이다.

2.2.7 좌-우 평행이동 (Left and Right Translations)

g, h \in G에 대해:

좌평행이동: L_g : G \to G, L_g(h) = gh

우평행이동: R_g : G \to G, R_g(h) = hg

좌불변 벡터장: X(gh) = dL_g(h)X(h)를 만족하는 벡터장

행렬 리 군에서: X(g) = gX(1)

2.2.8 수반 표현 (Adjoint Representations)

내부 자기동형사상: \Psi_g(h) = R_{g^{-1}}L_g(h) = ghg^{-1}

대수반 연산자 (Large Adjoint): \text{Ad}_g : G \times \mathfrak{g} \to \mathfrak{g}

\text{Ad}_g X := \frac{d}{dt}(g \cdot \exp(tX) \cdot g^{-1})|_{t=0} = gXg^{-1}

소수반 연산자 (Small adjoint): \text{ad} : \mathfrak{g} \to \mathfrak{gl}(\mathfrak{g})

\text{ad}_X Y = [X, Y]

Ad와 ad의 관계:

\text{Ad}_{(\exp tX)} = \exp(t \cdot \text{ad}_{(X)})

합성 규칙:

\text{Ad}_g \text{Ad}_h(X) = \text{Ad}_{gh}(X)

2.2.9 함수의 리 미분 (Lie Derivative)

X \in \mathfrak{g}이고 f : G \to \mathbb{R}가 해석적일 때:

\mathcal{L}_X f(g) := \lim_{t \to 0} \frac{f(g\exp(tX)) - f(g)}{t} = \frac{d}{dt}f(g\exp(tX))\bigg|_{t=0}

2.3 특수 유클리드 군 SE(3)

SE(3)는 로보틱스에서 가장 널리 사용되는 군으로, 이 섹션에서 자세히 다룬다.

2.3.1 SE(3)의 리 군 성질

SE(3)에서의 강체 운동

좌표계 \{A\} (관성 좌표계)에 대한 강체에 부착된 좌표계 \{B\}의 위치와 방향을 고려하자.

SE(3) = \{(p, R) : p \in \mathbb{R}^3, R \in SO(3)\} = \mathbb{R}^3 \rtimes SO(3)

원소 g = (p, R) \in SE(3)는:

강체의 배치(Configuration) 사양
좌표 변환 (한 프레임에서 다른 프레임으로)

점 q에 대한 강체 변환의 작용: g \circ q = p + Rq

동차 행렬 표현 (Homogeneous Matrix Representation)

\bar{g} = \begin{bmatrix} R & p \\ 0 & 1 \end{bmatrix}, \quad R \in SO(3), p \in \mathbb{R}^3

동차 좌표를 사용한 좌표 변환: \bar{q}_a = \begin{bmatrix} q_a \\ 1 \end{bmatrix} = \begin{bmatrix} R_{ab} & p_{ab} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} q_b \\ 1 \end{bmatrix} = \bar{g}_{ab}\bar{q}_b

SE(3)의 군 성질 확인:

닫힘: g_1, g_2 \in SE(3) \Rightarrow g_1g_2 \in SE(3)
항등원: I_4 \in SE(3)
역원: g^{-1} = \begin{bmatrix} R^T & -R^T p \\ 0 & 1 \end{bmatrix} \in SE(3)
결합법칙 성립

2.3.2 SE(3)의 리 대수 성질

\mathfrak{so}(3)와 \mathfrak{se}(3)의 Hat-map과 Vee-map

\mathfrak{so}(3)의 Hat-map \widehat{(\cdot)} : \mathbb{R}^3 \to \mathfrak{so}(3):

\hat{\omega} = -\hat{\omega}^T = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix} \in \mathbb{R}^{3 \times 3}

\hat{\omega}v = \omega \times v (벡터의 외적)

\mathfrak{se}(3)의 Hat-map \widehat{(\cdot)} : \mathbb{R}^6 \to \mathfrak{se}(3):

\hat{\xi} = \begin{bmatrix} \hat{\omega} & v \\ 0 & 0 \end{bmatrix} \in \mathfrak{se}(3) \subset \mathbb{R}^{4 \times 4}, \quad \forall \xi = \begin{bmatrix} v \\ \omega \end{bmatrix} \in \mathbb{R}^6

트위스트 (Twist)

\mathfrak{se}(3)의 원소를 트위스트 또는 유클리드 군의 (무한소) 생성자라고 부른다.

g \in SE(3)가 \hat{\xi} \in \mathfrak{se}(3)에 작용하는 수반 작용:

\text{Ad}_g \hat{\xi} = g\hat{\xi}g^{-1}

물체 속도 (Body Velocity)와 공간 속도 (Spatial Velocity)

시간에 따른 곡선 g_{ab}(t) = \begin{bmatrix} R_{ab}(t) & p_{ab}(t) \\ 0 & 1 \end{bmatrix}에 대해:

공간 속도:

\hat{V}^s_{ab} := \dot{g}_{ab}g^{-1}_{ab}

V^s_{ab} = \begin{bmatrix} v^s_{ab} \\ \omega^s_{ab} \end{bmatrix} = \begin{bmatrix} -\dot{R}_{ab}R^T_{ab}p_{ab} + \dot{p}_{ab} \\ (\dot{R}_{ab}R^T_{ab})^\vee \end{bmatrix}

물체 속도:

\hat{V}^b_{ab} := g^{-1}_{ab}\dot{g}_{ab}

V^b_{ab} = \begin{bmatrix} v^b_{ab} \\ \omega^b_{ab} \end{bmatrix} = \begin{bmatrix} R^T_{ab}\dot{p}_{ab} \\ (R^T_{ab}\dot{R}_{ab})^\vee \end{bmatrix}

속도 변환 (Adjoint Transformation):

V^s_{ab} = \text{Ad}_{g_{ab}} V^b_{ab}

\text{Ad}_g = \begin{bmatrix} R & \hat{p}R \\ 0 & R \end{bmatrix}, \quad g \in SE(3)

\text{Ad}^{-1}_g = \begin{bmatrix} R^T & -R^T\hat{p} \\ 0 & R^T \end{bmatrix} = \text{Ad}_{g^{-1}}

렌치 (Wrench)

렌치는 강체에 작용하는 힘과 모멘트의 쌍으로, 일반화된 힘이다:

F = \begin{bmatrix} f \\ \tau \end{bmatrix} \in \mathbb{R}^6

무한소 일:

\delta W = \langle V^b_{ab}, F^b \rangle = (v^{b^T}_{ab}f + \omega^{b^T}_{ab}\tau)

렌치의 좌표 변환:

F_c = \text{Ad}^T_{g_{bc}} F_b

\mathfrak{se}(3)에서 SE(3)로의 지수 사상

\hat{\xi} \in \mathfrak{se}(3)와 \theta \in \mathbb{R}에 대해:

\exp(\hat{\xi}\theta) = \exp\left(\begin{bmatrix} \hat{\omega} & v \\ 0 & 0 \end{bmatrix}\theta\right) \in SE(3)

변환 g = \exp(\hat{\xi}\theta)는 초기 좌표 p(0) \in \mathbb{R}^3를 강체 운동 후의 좌표 p(\theta)로 매핑한다: p(\theta) = \exp(\hat{\xi}\theta)p(0)

2.3.3 정기구학 (Forward Kinematics)

매니퓰레이터의 정기구학은 지수의 곱 공식 (Product of Exponentials)으로 주어진다:

g(\Theta) = e^{(\hat{\xi}_1\theta_1)}e^{(\hat{\xi}_2\theta_2)} \cdots e^{(\hat{\xi}_n\theta_n)}g(0)

여기서:

g(\theta): 공간 좌표계에서 엔드이펙터의 동차 표현
\xi_i \in \mathbb{R}^6: 공간 좌표계에서 표현된 트위스트
\theta_i \in \mathbb{R}: i번째 관절의 관절 각도

3. 등변 딥러닝 (Equivariant Deep Learning)

등변 딥러닝은 주로 2D 이미지나 3D 포인트 클라우드와 같은 시각 입력을 처리하는 데 사용된다. 이 장에서는 등변성의 개념과 등변 신경망 구조를 소개한다.

3.1 정규 그룹 CNN (Regular Group CNNs)

3.1.1 표준 CNN: 상호상관 커널과 가중치 공유

상호상관(Cross-correlation) 연산:

입력 이미지 f(x)와 상호상관 커널 k(x)의 상호상관:

y(x) = (k \star f)(x) = \int_{\mathbb{R}^n} f(\tilde{x})k(\tilde{x} - x)d\tilde{x}

또는 컨볼루션 커널 \hat{k}(x)를 사용하면:

y(x) = (\hat{k} * f)(x) = \int_{\mathbb{R}^n} f(\tilde{x})\hat{k}(x - \tilde{x})d\tilde{x}

여기서 k(x) = \hat{k}(-x)이다.

좌정칙 표현 (Left-regular Representation):

군 G가 함수 f(x)에 작용하는 방식:

L_g(f)(x) = g \circ f(x) = f(g^{-1} \circ x)

이 정의에서: L_{g_1g_2}(f)(x) = f((g_1g_2)^{-1} \circ x) = f(g_2^{-1}g_1^{-1} \circ x)

가중치 공유 (Weight-sharing):

평행이동군 (\mathbb{R}^n, +)의 좌정칙 표현을 상호상관 커널에 적용:

T_x(k)(\tilde{x}) := L_x(k)(\tilde{x}) = k(\tilde{x} - x)

상호상관을 내적으로 표현:

y(x) = (k \star f)(x) = \langle T_x(k), f \rangle_{L^2(\mathbb{R}^n)}

이 형태는 CNN이 템플릿 매칭을 수행함을 보여준다. 같은 커널 가중치를 여러 위치에서 공유하여 효율적인 학습이 가능하다.

표준 CNN의 문제점: 회전에 대한 가중치 공유가 없어서, 다양한 방향의 비슷한 필터들이 중복 생성된다.

3.1.2 SE(2) 정규 그룹 CNN

2D 회전에 대한 가중치 공유를 통합하기 위해, G-CNN은 2D 회전-평행이동 군 SE(2)에서의 컨볼루션 개념을 도입한다.

SE(2) 리프팅 상호상관 (Lifting Correlation):

\mathbb{R}^2에서 SE(2) 공간으로의 리프팅:

f_{SE(2)}(g) = y_{SE(2)}(x, \theta) = (k \star_{SE(2)} f)(x, \theta)

= \langle L_{(x,\theta)}k, f \rangle_{L^2(\mathbb{R}^2)} = \int_{\mathbb{R}^2} k(R_\theta^{-1}(\tilde{x} - x))f(\tilde{x})d\tilde{x}

SE(2) 정규 그룹 상호상관:

리프팅 후, SE(2)의 고차원 특징 맵에서 그룹 상호상관 수행:

y(g) = \int_{SE(2)} k(g^{-1} \cdot \tilde{g})f_{SE(2)}(\tilde{g})d\tilde{g}

= \int_{\mathbb{R}^2} \int_{S^1} k(R_\theta^{-1}(\tilde{x} - x), \tilde{\theta} - \theta)f_{SE(2)}(\tilde{x}, \tilde{\theta})d\tilde{x}d\tilde{\theta}

실제 구현: 연속적인 SE(2) 군을 유한 부분군 \mathbb{R}^2 \rtimes C_N으로 근사한다. 여기서 C_N은 차수 N의 순환군이다.

3.1.3 등변 사상 (Equivariant Maps)

G가 리 군이고, M과 N이 매끄러운 다양체일 때, 사상 \Phi : M \to N이 G-작용에 대해 등변이라 함은:

\Phi(g \circ p) = g \circ \Phi(p) \quad \text{(좌작용의 경우)}

\Phi(p \circ g) = \Phi(p) \circ g \quad \text{(우작용의 경우)}

등변성의 의미:

입력 변환에 의해 정보가 손실되지 않음
출력이 입력 변환에 대응하는 위치로 이동
변환에 대한 가중치 공유 가능 → 학습 파라미터 수 감소

3.2 조향 가능 그룹 CNN (Steerable Group CNNs)

조향 가능(Steerable) 특징 벡터를 사용하여 더 효율적인 등변 CNN을 구성할 수 있다. 조향 가능 방법은 SO(n)의 이산화를 피하고, 기약 표현을 활용하여 리 군 위의 푸리에 이론을 사용한다.

3.2.1 구면 조화 함수 (Spherical Harmonics, SH)

구면 조화 함수는 조향 가능 함수의 이론적 기초를 제공하며, SO(3) 변환의 기저 함수 역할을 한다.

Y^l_m(\theta, \phi) = Ne^{im\phi}P^l_m(\cos\theta)

여기서:

\theta, \phi: 방위각과 경도각
P^l_m: 연관 르장드르 다항식
l \in \{0, 1, 2, \ldots\}: 차수 (degree)
m \in \{-l, \ldots, l\}: 순서 (order)

구면 조화 함수가 펼치는 부분 표현 공간:

V_0 = \text{Span}\{Y^0_0(n)\} V_1 = \text{Span}\{Y^1_{-1}(n), Y^1_0(n), Y^1_1(n)\} V_k = \text{Span}\{Y^k_{-k}(n), Y^k_{-k+1}(n), \ldots, Y^k_k(n)\}

V_l을 type-l (또는 spin-l) 벡터장이라 부른다.

Type	차원	물리적 의미
Type-0	1	스칼라 (회전에 불변)
Type-1	3	3차원 벡터
Type-2	5	고차 텐서

구면 조화 함수의 핵심 성질 - Wigner-D 행렬에 의한 등변 변환:

(2l+1)차원 벡터장: Y^l = [Y^l_{-l}, Y^l_{-l+1}, \ldots, Y^l_{l-1}, Y^l_l]^T

Y^l\left(R\frac{x}{\|x\|}\right) = D^l(R)Y^l\left(\frac{x}{\|x\|}\right)

여기서 D^l(R)은 R \in SO(3)의 차수 l Wigner-D 행렬 표현이다.

3.2.2 Wigner-D 행렬

SO(3)의 직교 기저로서의 Wigner-D 행렬:

SO(3) 위의 임의의 함수 h는 Wigner-D 행렬의 푸리에 급수로 표현 가능:

h(R) = \sum_{l=0}^{\infty} \sum_{m=-l}^{l} \sum_{n=-l}^{l} \hat{h}^{(l)}_{mn} D^l_{mn}(R) = \sum_{l=0}^{\infty} \text{tr}[\hat{h}^{(l)}(D^l(R))^T]

SO(3) 군 표현으로서의 Wigner-D 행렬:

SO(3)의 임의의 표현 D(R)은 기약 표현 D^l(R)의 직접합으로 약분 가능:

D(R) = U\left[\bigoplus_{l=1}^{N} D^l(R)\right]U^{-1}, \quad \forall R \in SO(3)

3.2.3 조향 가능 함수와 벡터

조향 가능 함수: 변환군 G에 대해, 임의의 변환 g \in G가 유한 기저 함수 집합 \{\phi_i\}의 선형 결합으로 표현 가능:

L_g k = \sum_{i=1}^{n} \alpha_i(g)\phi_i = \alpha^T(g)\Phi

조향 가능 특징 벡터: Wigner-D 행렬에 의해 변환되는 벡터

Type-l 조향 가능 벡터 공간 V_l은 (2l+1)차원이며, 차수 l의 Wigner-D 행렬에 의해 작용을 받는다.

예: u가 V_3의 type-3 벡터이면, g \in SO(3)에 의해 u \to D^3(g)u로 변환

3.2.4 조향 가능 그룹 컨볼루션

구면 조화 기저로 전개된 3D 컨볼루션 커널 (차수 L까지):

k(x) = k_c(\|x\|)(x) := \sum_{l=0}^{L} \sum_{m=-l}^{l} c^l_m(\|x\|)Y^l_m\left(\frac{x}{\|x\|}\right)

이 커널은 계수 c의 SO(3) 표현 D(R)에 의해 조향 가능:

L_g k(x) = k(g^{-1}x) = k_c(R^{-1}x) = k_{D(R)c(\|x\|)}(x)

SE(3) 리프팅 컨볼루션:

y(g) = y(x, R) = \langle L_g k, f \rangle_{L^2(\mathbb{R}^3)}

= D(R)^T \int_{\mathbb{R}^3} c(\|\tilde{x} - x\|)^T \Phi\left(\frac{\tilde{x} - x}{\|\tilde{x} - x\|}\right)f(\tilde{x})d\tilde{x}

= D(R)^T \hat{f}^\Phi_c(x)

여기서 \hat{f}^\Phi_c(x)는 응답의 조향 가능 벡터이다.

핵심: D(R)^T가 컨볼루션 적분 밖으로 나올 수 있어서, R에 대한 이산화 없이 y(g)를 g의 함수로 표현 가능하다.

3.2.5 클렙시-고르단 텐서곱 (Clebsch-Gordan Tensor Product)

조향 가능 입력과 출력 벡터 공간 사이를 매핑하는 조향 가능 선형 층에 사용된다.

두 조향 가능 벡터 u \in V_{l_1}와 v \in V_{l_2}에 대해, CG 텐서곱의 출력도 SO(3) 표현 D(R)로 조향 가능:

D(R)(u \otimes v) = (D^{l_1}(R)u) \otimes (D^{l_2}(R)v)

CG 텐서곱을 사용하여 텐서곱의 type-l 부분벡터의 m번째 성분 정의:

(u \otimes_{cg} v)^l_m = \sum_{m_1=-l_1}^{l_1} \sum_{m_2=-l_2}^{l_2} C^{(l,m)}_{(l_1,m_1)(l_2,m_2)} u_{m_1} v_{m_2}

여기서 C^{(l,m)}_{(l_1,m_1)(l_2,m_2)}는 클렙시-고르단 계수이다.

CG 텐서곱은 |l_1 - l_2| \leq l \leq l_1 + l_2가 아닌 경우 C^{(l,m)}_{(l_1,m_1)(l_2,m_2)} = 0이므로 일반적으로 희소하다.

3.3 SE(3)-등변 그래프 신경망

3D 포인트 클라우드는 RGBD 입력에서 생성되며, SE(3) 등변 그래프 신경망으로 효율적으로 처리할 수 있다.

SE(3)-등변 사상의 정의:

D_V(g)f(O_X | O_Y) = f(g \circ O_X | g \circ O_Y)

D_V(g) = I인 특수한 경우, 사상 f(O_X | O_Y)는 G-불변이라 한다.

SE(3)-등변 type-l 벡터장:

D^l(R)f(x | O_X) = f(Rx + p | g \circ O_X), \quad \forall g = (p, R) \in SE(3)

3.3.1 텐서장 신경망 (Tensor Field Networks, TFN)

TFN은 포인트 클라우드 입력에서 표현론적 벡터장을 생성하는 SE(3)-등변 모델이다.

특징 포인트 클라우드 입력: O_X = \{(x_1, f_1), \ldots, (x_M, f_M)\}

g = (p, R) \in SE(3)의 O_X에 대한 작용: g \circ O_X = \{(gx_1, D(R)f_1), \ldots, (gx_M, D(R)f_M)\}

입력 특징장: f^{(in)}(x | X) = \sum_{j=1}^{M} f_j \delta^{(3)}(x - x_j)

출력 특징장 (상호상관으로 생성): f^{(out)}(x | O_X) = \int_{\mathbb{R}^3} k(x - y)f^{(in)}(y | O_X)dy^3 = \sum_j k(x - x_j)f_j

컨볼루션 커널: [k^{(n',n)}(x)]_{m'm} = \sum_{J=|l_{n'} - l_n|}^{l_{n'} + l_n} \phi^{(n',n)}_J(\|x\|) \sum_{k=-J}^{J} C^{(l_{n'}, m')}_{(l_n, m)(J, k)} Y^J_k(x/\|x\|)

클렙시-고르단 계수의 인터트와이닝 성질로 인해: k^{(n',n)}(Rx) = D^{l_{n'}}(R) k^{(n',n)}(x) D^{l_n}(R)^{-1}

이 성질로 출력 특징장 f^{(out)}(x | O_X)가 SE(3)-등변임을 증명할 수 있다.

SE(3)-Transformers:

TFN의 변형으로 자기 주의(Self-attention) 메커니즘을 추가:

f_{(out),i} = \sum_{j \neq i} \alpha_{ij} k(x - x_j)f_j + \bigoplus_{n'=1}^{N'} \sum_{n=1}^{N} k^{(n',n)}_{(S)} f^{(n)}_j

여기서 \alpha_{ij}는 type-0 (스칼라) 자기 주의, k^{(n',n)}_{(S)}는 자기 상호작용 항이다.

3.3.2 텐서곱의 계산 복잡도 처리

등변 구면 채널 네트워크 (eSCN):

TFN의 원래 텐서곱 연산과 수학적으로 동등하면서 효율성을 개선한 대안을 제시한다.

텐서곱 복잡도: O(L^6) \to O(L^3) (여기서 L은 최고 특징 타입)
훨씬 고주파 특징 사용 가능 → 로봇 조작 작업의 정확도 향상

Gaunt 텐서곱:

클렙시-고르단 계수를 세 구면 조화 함수의 곱의 적분인 Gaunt 계수와 연결하여 복잡도를 O(L^6)에서 O(L^3)으로 감소시킨다.

3.4 PointNet 기반 등변 신경망

PointNet: 포인트 클라우드를 직접 처리하도록 설계된 신경망 아키텍처로, 입력 점들의 순서에 관계없이 일관된 출력을 보장하는 순열 불변성을 보장한다.

Vector Neurons (VN): 스칼라 뉴런을 3D 벡터 뉴런으로 확장하여 SO(3)-등변 신경망 구성을 가능하게 한다.

VN은 다음과 같은 SO(3)-등변 빌딩 블록을 제공한다:

선형 층
비선형성
풀링
정규화

VN 프레임워크를 기반으로 한 VN-PointNet은 SO(3)-등변 PointNet이다.

4. 로보틱스에서의 등변 딥러닝

등변 신경망은 데이터 수집이 비용이 많이 들고 대규모 데이터셋이 필요한 로봇 학습에서 데이터 효율성과 일반화 성능을 크게 향상시킬 수 있다.

4.1 모방 학습 (Imitation Learning)

모방 학습은 원하는 행동을 보여줌으로써 로봇을 가르치는 방법으로, 자세한 프로그래밍이나 수고로운 보상 함수 엔지니어링을 완화한다. 그러나 데이터 수집 비용이 방법의 확장성과 효율성을 저하시킨다.

4.1.1 등변 기술자장 (Equivariant Descriptor Fields, EDF)

Neural Descriptor Fields (NDF)는 Vector Neurons를 사용한 카테고리 수준 기술자로 객체 표현을 구현하여 시뮬레이션과 실제 환경 모두에서 5-10개의 시연으로 조작 작업 학습을 가능하게 한다.

EDF는 Equiformer와 SE(3)-Transformer의 국소성을 활용하여 지역 등변성을 달성한다. 이를 통해 사전 훈련과 객체 분할 없이 종단간 훈련이 가능하다.

SE(3) 위의 이중등변 에너지 기반 모델:

P(g | O^{scene}, O^{grasp}) = \frac{\exp(-E(g | O^{scene}, O^{grasp}))}{Z}

Z = \int_{SE(3)} dg \exp(-E(g | O^{scene}, O^{grasp}))

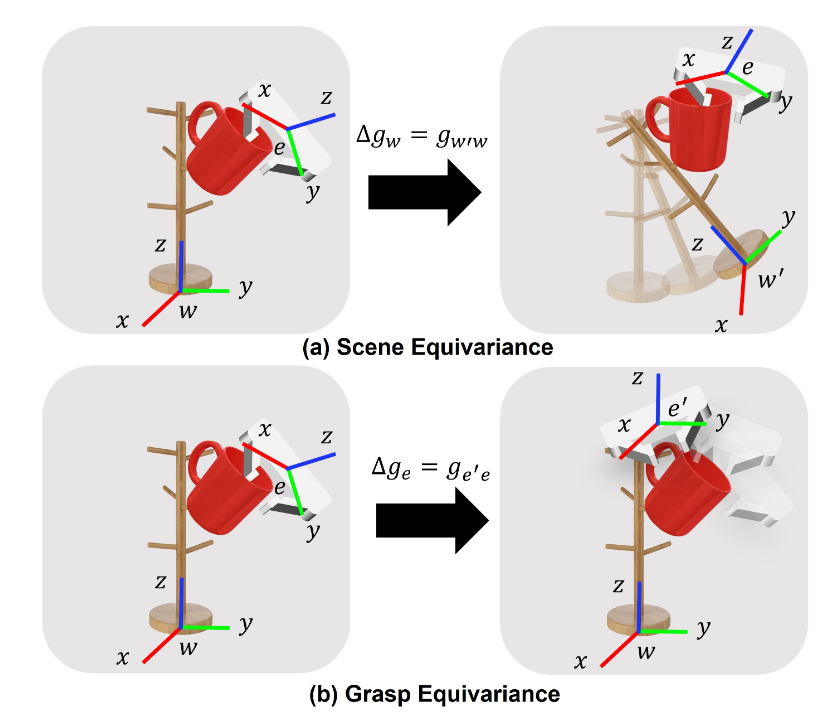
이중등변(Bi-equivariance) 조건:

P(g | O^{scene}, O^{grasp}) = P(\Delta g_w g | \Delta g_w \circ O^{scene}, O^{grasp}) = P(g\Delta g_e^{-1} | O^{scene}, \Delta g_e \circ O^{grasp})

여기서 \Delta g_w는 월드 프레임 변환, \Delta g_e는 엔드이펙터 프레임 변환이다.

에너지 함수:

E(g | O^{scene}, O^{grasp}) = \int_{\mathbb{R}^3} d^3x \, \rho(x | O^{grasp}) \|\phi(gx | O^{scene}) - D(R)\psi(x | O^{grasp})\|^2

여기서:

\rho(x | O^{grasp}): 쿼리 밀도 (SE(3)-등변 비음수 스칼라장)
\phi(gx | O^{scene}): 키 EDF
\psi(x | O^{grasp}): 쿼리 EDF

4.1.2 Diffusion-EDF

Diffusion-EDF는 이중등변성과 로봇 조작의 국소성을 활용하여 EDF의 훈련 시간을 개선하면서 종단간 훈련 방식과 데이터 효율성을 유지한다.

이중등변 스코어 함수:

s(\Delta g g | \Delta g \circ O^{scene}, O^{grasp}) = s(g | O^{scene}, O^{grasp})

s(g\Delta g^{-1} | O^{scene}, \Delta g \circ O^{grasp}) = [\text{Ad}_{\Delta g}]^{-T} s(g | O^{scene}, O^{grasp})

\text{Ad}_g = \begin{bmatrix} R & \hat{p}R \\ 0 & R \end{bmatrix}

스코어 모델:

s_t(g | O^{scene}, O^{grasp}) = [s_{\nu;t} \oplus s_{\omega;t}](g | O^{scene}, O^{grasp})

여기서 s_{\nu;t}는 평행이동 스코어, s_{\omega;t}는 회전 스코어이다.

4.1.3 RiEMann

RiEMann은 거의 실시간 SE(3)-등변 로봇 조작 프레임워크이다.

SE(3)-Transformer로 어포던스 맵 \phi(x | O_X) 학습
어포던스 맵에서 관심 영역 B_{ROI} 추출
계산 복잡도와 메모리 사용량 감소

출력 설계:

평행이동 행동 네트워크: type-0 벡터장 하나
방향 네트워크: type-1 벡터장 세 개 → IMGS 직교화로 회전 행렬 예측

4.1.4 Fourier Transporter

3D 컨볼루션과 회전의 푸리에 표현을 사용한 SE(3) 이중등변 모델이다.

픽 네트워크:

f_{pick} : o_t \mapsto p(a_{pick} | o_t)

픽 포즈 분포는 관찰에 대한 변환을 따라야 한다:

f_{pick}(g \circ o_t) = \text{Ind}_\rho(g)f_{pick}(o_t), \quad \forall g \in SE(3)

플레이스 네트워크:

f_{place} : (c, o_t) \to p(a_{place} | o_t, a_{pick})

이중등변 제약:

f_{place}(g_1 \circ c, g_2 \circ o_t) = \text{Ind}_\rho(g_2)\rho_R(g_1^{-1})f_{place}(c, o_t)

동적 커널: 밀집 특징 맵을 유한 회전으로 리프팅하고 푸리에 변환하여 채널 공간으로 변환

\mathcal{L}^\uparrow[f](x) = \{f(R_1^{-1}x), f(R_2^{-1}x), \ldots, f(R_m^{-1}x)\}

\kappa(c) = \mathcal{F}^+[\mathcal{L}^\uparrow(\psi(c))]

4.2 등변 강화 학습 (Equivariant Reinforcement Learning)

많은 등변 강화 학습 방법은 군불변 마르코프 결정 과정 (Group-invariant MDP)의 기본 개념에 기반한다.

\mathcal{M}_G = (S, A, P, R, G)

4.2.1 군불변 MDP의 조건

보상 함수: R(s, a) = R(g \circ s, g \circ a)
전이 확률: P(s' | s, a) = P(g \circ s' | g \circ s, g \circ a)

4.2.2 결과적 성질

군불변 성질로 인해:

최적 Q 함수: Q^*(s, a) = Q^*(g \circ s, g \circ a) (군불변)
최적 정책: \pi^*(g \circ s) = g \circ \pi^*(s) (등변)

4.2.3 증명 개요

벨만 최적 방정식: Q^*(s, a) = R(s, a) + \gamma \sup_{a'} \int_{s'} ds' P(s' | s, a)Q^*(s', a')

변환된 상태-행동 쌍에 대해: Q^*(g \circ s, g \circ a) = R(s, a) + \gamma \sup_{a'} \int_{s'} ds' P(s' | s, a)Q^*(g \circ s', g \circ a')

\bar{Q}(s, a) = Q(g \circ s, g \circ a)를 정의하면: \bar{Q}^*(s, a) = R(s, a) + \gamma \sup_{a'} \int_{s'} ds' P(s' | s, a)\bar{Q}^*(s', a')

벨만 최적 방정식의 유일성에 의해: Q^*(s, a) = Q^*(g \circ s, g \circ a)

정책의 등변성: \pi^*(g \circ s) = \arg\max_a Q^*(g \circ s, a) = g \circ \arg\max_{\bar{a}} Q^*(s, \bar{a}) = g \circ \pi^*(s)

4.2.4 응용

SO(2)-등변 Q 학습: DQN과 SAC에 등변 네트워크 적용
시각-힘 문제: 힘 입력과 시각 입력을 활용한 등변 정책 학습
POMDP로의 확장: 부분 관측 가능 MDP에서의 등변 강화 학습
오프라인 강화 학습: Conservative Q-Learning과 Implicit Q-Learning에 등변 네트워크 적용

5. 기하학적 임피던스 제어 (Geometric Impedance Control)

이 섹션에서는 기하학적 임피던스 제어(GIC)를 소개하고, 이것이 SE(3) 군 등변 제어 법칙임을 보인다.

5.1 매니퓰레이터 동역학

5.1.1 관절 공간에서의 매니퓰레이터 동역학

M(q)\ddot{q} + C(q, \dot{q})\dot{q} + G(q) = \tau + \tau_e

여기서:

q \in \mathbb{R}^n: 관절 위치 좌표
\dot{q} \in \mathbb{R}^n: 관절 속도
\ddot{q} \in \mathbb{R}^n: 관절 가속도
M(q) \in \mathbb{R}^{n \times n}: 관성 행렬
C(q, \dot{q}) \in \mathbb{R}^{n \times n}: 코리올리 행렬
G(q) \in \mathbb{R}^n: 중력 힘 벡터
\tau \in \mathbb{R}^n: 제어 입력 관절 토크
\tau_e \in \mathbb{R}^n: 외부 교란

5.1.2 SE(3) 위의 작업 공간에서의 매니퓰레이터 동역학

작업 공간 공식을 사용한 물체 프레임 속도 V^b 기반 동역학:

\tilde{M}(q)\dot{V}^b + \tilde{C}(q, \dot{q})V^b + \tilde{G}(q) = \tilde{T} + \tilde{T}_e

여기서: \tilde{M}(q) = J_b(q)^{-T}M(q)J_b(q)^{-1} \tilde{C}(q, \dot{q}) = J_b(q)^{-T}(C(q, \dot{q}) - M(q)J_b(q)^{-1}\dot{J})J_b(q)^{-1} \tilde{G}(q) = J_b(q)^{-T}G(q), \quad \tilde{T} = J_b(q)^{-T}T, \quad \tilde{T}_e = J_b(q)^{-T}T_e

J_b는 물체 프레임 야코비안 행렬: V^b = J_b\dot{q}

5.2 오차 함수: SE(3) 위의 거리 유사 메트릭

5.2.1 배치 오차 (Configuration Error)

원하는 배치 g_d = (p_d, R_d)와 현재 배치 g = (p, R) 사이의 변환 행렬:

g_{de} = g_d^{-1}g

5.2.2 행렬 군 관점에서의 오차 함수

프로베니우스 노름을 기반으로 한 오차 함수:

\Psi_1(g, g_d) = \frac{1}{2}\|I - g_d^T g\|_F^2

= \text{tr}(I - R_d^T R) + \frac{1}{2}(p - p_d)^T(p - p_d)

SO(3)에서의 오차 함수: \Psi(R, R_d) = \text{tr}(I - R_d^T R) = \frac{1}{2}\|I - R_d^T R\|_F^2

5.2.3 리 대수 관점에서의 오차 함수

배치 오차의 벡터 표현:

\xi_{de} = \log(g_{de})^\vee = \begin{bmatrix} \hat{\psi}_{de} & b_{de} \\ 0 & 0 \end{bmatrix}^\vee = \begin{bmatrix} b_{de} \\ \psi_{de} \end{bmatrix}

여기서: \hat{\psi}_{de} = \log(R_d^T R), \quad b_{de} = A^{-1}(\psi_{de})R_d^T(p - p_d)

A^{-1}(\psi) = I - \frac{1}{2}\hat{\psi} + \frac{2\sin\|\psi\| - \|\psi\|(1 + \cos\|\psi\|)}{2\|\psi\|^2 \sin\|\psi\|}\hat{\psi}^2

\mathfrak{se}(3) 위의 내적 (좌불변 리만 메트릭):

\langle\hat{\xi}_1, \hat{\xi}_2\rangle_{(P,I)} = \xi_1^T P \xi_2

리 대수 관점의 오차 함수:

\Psi_2(g, g_d) = \langle g_{de}\hat{\xi}_{de}, g_{de}\hat{\xi}_{de}\rangle_{(0.5I, g_{de})} = \frac{1}{2}\|\psi_{de}\|^2 + \frac{1}{2}\|b_{de}\|^2

5.3 SE(3) 위의 오차 벡터

5.3.1 위치 오차 벡터

기하학적 일관 오차 벡터 (GCEV):

e_G = \begin{bmatrix} e_p \\ e_R \end{bmatrix} = \begin{bmatrix} R^T(p - p_d) \\ (R_d^T R - R^T R_d)^\vee \end{bmatrix} \in \mathbb{R}^6

리 대수 기반 오차 벡터: 배치 오차의 로그 맵

\xi_{de} = \log(g_{de})^\vee

5.3.2 속도 오차 벡터

두 접선 벡터 \dot{g} \in T_g SE(3)와 \dot{g}_d \in T_{g_d} SE(3)가 다른 접선 공간에 있으므로 직접 비교할 수 없다.

원하는 속도의 변환:

\hat{V}^*_d = g_{ed}\hat{V}^b_d g^{-1}_{ed}, \quad \text{where } g_{ed} = g^{-1}g_d

V^*_d = \text{Ad}_{g_{ed}} V^b_d

속도 오차 벡터:

e_V = \begin{bmatrix} v^b \\ w^b \end{bmatrix} - \begin{bmatrix} R^T R_d v_d + R^T R_d \hat{\omega}_d R_d^T(p - p_d) \\ R^T R_d \omega_d \end{bmatrix} = \begin{bmatrix} e_v \\ e_\Omega \end{bmatrix}

5.4 SE(3) 위의 에너지 함수

5.4.1 위치 에너지 함수

행렬 군 관점의 위치 에너지:

P_1(g, g_d) = \text{tr}(K_R(I - R_d^T R)) + \frac{1}{2}(p - p_d)^T R_d K_p R_d^T(p - p_d)

리 대수 관점의 위치 에너지:

P_2(g, g_d) = \langle\hat{\xi}_{de}, \hat{\xi}_{de}\rangle_{(0.5K_\xi, I)} = \frac{1}{2}\xi_{de}^T K_\xi \xi_{de}

P_1(g, g_d)와 P_2(g, g_d)는 모두 좌불변, 양정치, 이차 형태이다.

5.4.2 운동 에너지

K(t, q, \dot{q}) = \frac{1}{2}e_V^T \tilde{M} e_V

5.5 기하학적 임피던스 제어

5.5.1 소산 제어 법칙으로서의 임피던스 제어

전체 기계적 에너지 함수 (리아푸노프 함수):

V_i(t, q, \dot{q}) = K(t, q, \dot{q}) + P_i(t, q), \quad i \in \{1, 2\}

소산 제어 법칙의 원하는 성질:

\dot{V}_i = -e_V^T K_d e_V

임피던스 제어 법칙:

\tilde{T}_i = \tilde{M}\dot{V}^*_d + \tilde{C}V^*_d + \tilde{G} - f_{G,i} - K_d e_V, \quad i \in \{1, 2\}

여기서 f_{G,i} \in \mathbb{R}^6:

f_{G,1} = \begin{bmatrix} f_p \\ f_R \end{bmatrix} = \begin{bmatrix} R^T R_d K_p R_d^T(p - p_d) \\ (K_R R_d^T R - R^T R_d K_R)^\vee \end{bmatrix}

f_{G,2} = K_\xi \xi_{de}

5.5.2 기하학적 임피던스 제어는 SE(3)-등변 제어

GIC의 중요한 장점은 공간 프레임에서 기술할 때 SE(3) 등변이라는 것이다.

f_{G,1}의 좌불변성:

f_{G,1}(g_l g, g_l g_d) = \begin{bmatrix} (R_l R)^T R_l R_d K_p(R_l R_d)^T(R_l p + p_l - R_l p_d - p_l) \\ (K_R(R_l R_d)^T R_l R - (R_l R)^T R_l R_d K_R)^\vee \end{bmatrix}

= \begin{bmatrix} R^T R_d K_p R_d(p - p_d) \\ (K_R R_d R - R^T R_d K_R)^\vee \end{bmatrix} = f_{G,1}(g, g_d)

f_{G,2}의 좌불변성:

f_{G,2}(g_l g, g_l g_d) = K_\xi \log((g_l g_d)^{-1}(g_l g_e)) = K_\xi \log(g_d^{-1}g_e) = K_\xi \xi_{de}

SE(3)-등변 정책을 위한 일반 레시피:

정책이 좌불변이어야 함
정책이 물체 프레임 좌표에서 기술되어야 함

6. 향후 연구 방향 (Future Works)

6.1 비전에서 힘까지의 SE(3)-등변성

현재의 비전 기반 접근법은 “모든 조작이 픽앤플레이스 시퀀스로 간주될 수 있다”는 철학에 기반한다. 그러나 많은 실제 작업은 힘 상호작용과 컴플라이언스가 필요하다.

예시: - 병뚜껑 돌려 열기 - 볼트-너트 조립 - 타이트 핏 조립

힘(또는 렌치)은 SE(3) 다양체의 쌍대 공간에서 대수반 맵에 의해 조향되는 두 개의 type-1 벡터로 해석될 수 있다.

6.2 로보틱스와 시스템에서의 대칭성 깨짐

대칭성이 깨지는 원인들:

운동학적 제약: 매니퓰레이터가 특이 배치에 접근할 때
제어 입력 제약: 입력에 제약이 있는 제어 시스템
관찰 공간의 불완전성: 기울어진 카메라 각도, 폐색

군불변 MDP에서의 대칭성 깨짐:

군불변 MDP는 군불변 보상 함수와 전이 확률을 가정하지만, 로봇 매니퓰레이터의 운동학적 제약 등에 의해 손상될 수 있다.

7. 결론 (Conclusions)

이 튜토리얼 서베이 논문에서는 로보틱스 응용을 위한 기하학적 딥러닝과 제어의 최신 발전을 검토했다.

주요 내용:

매니퓰레이터 엔드이펙터의 SE(3) 다양체 구조에 대한 수학적 배경 제시
SE(3)-등변 딥러닝의 공식화와 이론, 백본 신경망 소개
모방 학습과 강화 학습에 활용되는 SE(3)-등변 모델의 최신 연구 소개
SE(3)-등변 학습 모듈의 저수준 제어 층으로 사용될 수 있는 SE(3)-등변 제어 방법 제시
등변 방법의 한계와 향후 연구 방향 논의

8. 부록 (Appendix)

A.1 매끄러운 다양체 (Smooth Manifolds)

A.1.1 접선 공간과 쌍대 공간

접선 공간 T_p M: 다양체 M 위의 점 p에서 모든 접선 벡터의 집합

좌표 차트 (x^1, \ldots, x^n)에서 T_p M의 기저: X_p = \sum_{i=1}^{n} X^i \frac{\partial}{\partial x^i} = X^i \frac{\partial}{\partial x^i}

쌍대 공간 (Cotangent Space) T^*_p M: 접선 공간의 쌍대 공간, 모든 선형 범함수의 집합

쌍대 기저: \{dx^1, \ldots, dx^n\}

dx^i\left(\frac{\partial}{\partial x^j}\right) = \delta^i_j

접선 다발 (Tangent Bundle): TM = \bigsqcup_{p \in M} T_p M

A.1.2 매끄러운 사상의 미분

F : M \to N이 매끄러운 사상일 때, p에서의 미분:

dF_p : T_p M \to T_{F(p)} N

dF_p(X_p)(f) = X_p(f \circ F)

국소 좌표에서: dF_p(X_p) = \left(\frac{\partial F^j(x)}{\partial x^i} X^i\right)\bigg|_p \frac{\partial}{\partial y^j}\bigg|_{F(p)}

A.1.3 푸시포워드와 풀백

푸시포워드 (Pushforward): F가 미분동형사상일 때: (F_* X)_q = dF_{F^{-1}(q)}(X_{F^{-1}(q)}) = dF_p(X_p)

풀백 (Pullback): 쌍대 벡터장 \omega에 대해: (F^* \omega)_p = dF^*_{F(p)}(\omega_{F(p)})

A.1.4 벡터장의 리 미분

V \in \mathfrak{X}(M)의 플로우 F_t에 대해, 벡터장 W의 V에 대한 리 미분:

(\mathcal{L}_V W)_p := \frac{d}{dt} d(F_{-t})_{F_t(p)}(W_{F_t(p)})\bigg|_{t=0}

= [V, W]_p

A.2 구면 조화 함수 (Spherical Harmonics)

구면 조화 함수는 구면 좌표계에서 라플라스 방정식을 풀 때 자연스럽게 나타난다.

라플라스 방정식: \nabla^2 f(x, y, z) = 0

구면 좌표로 변환하고 변수 분리: f(r, \theta, \phi) = R(r)Y(\theta, \phi)

구면 조화 함수: Y^l_m(\theta, \phi) = Ne^{im\phi}P^l_m(\cos\theta)

라플라스 방정식의 일반해: f(r, \theta, \phi) = \sum_{l=0}^{\infty} \sum_{m=-l}^{l} f^l_m r^l Y^l_m(\theta, \phi)

A.3 등변 구면 채널 네트워크 (eSCN)

eSCN은 메시지 패싱 방향이 y축에 정렬된 참조 프레임에서 클렙시-고르단 계수의 희소성을 활용한다.

정렬된 참조 프레임에서의 구면 조화: Y^l_m(\hat{e}_y) = \delta_{m0}

회전-적용-역회전 전략: f^{(out)}(x) = \sum_i D(R_y^{-1})k(\|x - x_j\|\hat{e}_y)D(R_y)f_j

이를 통해 SO(2) 컨볼루션 (스펙트럼 도메인에서 점별 곱셈)으로 해석할 수 있다.

A.4 우불변 메트릭에 대한 코멘트

SE(3)에서는 이중불변(bi-invariance)이 불가능하고, 좌불변 또는 우불변 중 하나만 만족할 수 있다.

우불변 오차 함수: \Psi^R(gg_r, g_d g_r) = \frac{1}{2}\|I - gg_r g_r^{-1}g_d^{-1}\|_F^2 = \Psi^R(g, g_d)

\Psi^R(g, g_d) = \text{tr}(I - RR_d^T) + \frac{1}{2}(p - RR_d^T p_d)^T(p - RR_d^T p_d)

우불변에서는 평행이동 성분이 회전의 영향을 받지만, 좌불변에서는 평행이동이 회전과 독립적이다.

우불변 오차 벡터: e^R_G = \begin{bmatrix} e^R_p \\ e^R_R \end{bmatrix} = \begin{bmatrix} (p - RR_d^T p_d) \\ (RR_d^T - R_d R^T)^\vee \end{bmatrix}

e^R_p = R(R^T p - R_d^T p_d)

좌불변 오차 벡터 e^L_p = R^T(p - p_d)와의 핵심 차이:

우불변 오차 벡터는 공간 프레임에 의존
좌불변 오차 벡터는 독립적

이중불변이 불가능하므로 특정 불변성의 한계를 해결하는 데 집중하는 것으로 충분하다.

📝 핵심 요약

개념	핵심 내용
SE(3)	3D 공간의 모든 강체 변환 (회전 + 평행이동)을 나타내는 군
등변성	입력 변환이 출력에서도 동일하게 나타나는 성질
불변성	입력 변환에도 출력이 변하지 않는 성질
조향 가능 특징	Wigner-D 행렬에 의해 변환되는 특징 벡터
TFN	SE(3)-등변 그래프 신경망의 기초 아키텍처
이중등변성	장면과 그래스프 모두에 대한 등변성
GIC	SE(3) 다양체 위에서 정의된 기하학적 임피던스 제어